八年级上数学测试（一次函数）
一、选择题(每题3分，共30分)
1、下列函数 (1)
(2)
(3)
(4)
中，是一次函数的有
（ ）
A.3个 B.2个 C.1个 D.0个
2、函数
中自变量
的取值范围是
（ ）
A．
B.
C.
且 D.且
3、直线
,,
共同具有的特征是 （ ）
A.经过原点
B.与
轴交于负半轴
C.随
增大而增大
D.随增大而减小
4.函数 y = x图象向下平移 2 个单位长度后，对应函数关系式是 ( )
A．
B．
C．
D．
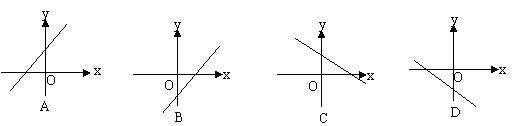5.已知正比例函数
的函数值随的增大而增大，则一次函数
的图象大致是
( )
6.一次函数
，经过（1，1），(2，
) ，则k与b的值为 ( )
A．
B．
C．
D．
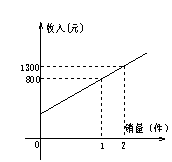
7．某公司市场营销部的个人月收入与其每月的销售量成一次函数关系，其图象如图所示，由图中给出的信息可知，营销人员没有销售时的收入是( )
A.310元 B．300元 C.290元 D．280元
8.直线
经过
和
,则
与
的大小关系是 （ ）
A. 
B. 
C.
D.无法确定
9. 无论
为何值,直线
与
的交点不可能在 （ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
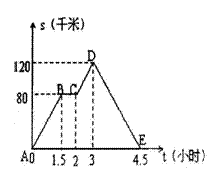10．如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120千米；②汽车在行驶途中停留了0.5小时；③汽车在整个行驶过程中的平均速度为30千米／时；④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少．其中正确的说法共有( )
A.1个 B．2个 C．3个 D．4个
二、填空题(每题3分，共30分)
11.若函数
是正比例函数，则的值是
.
12. 若函数
图象经过点（1，2），则m=
13. 对于一次函数
，当______时，图象在轴下方.
14. 直线
与x轴交点坐标是_______,与y轴交点坐标是_______.
15.若点P(a，b)在第二象限内，则直线y＝ax＋b不经过第_______限．
16. 一次函数y=-x+a与y=x+b的交点坐标为（m，8），则a+b=_____．
17. 如果A(－1，2)，B(2，－1)，C(m，m)三点在同一条直线上，则m的值等于______．
18. 一次函数
的图象与坐标轴所围成的三角形面积是
.
19.直线
与直线
相交于轴，且与直线
平行，则直线的解析式为____________.
20. 已知直线
和
的交点在第一象限，请写出满足条件的b的值为_____（只写一个）.
三、解答题(共60分)
21、(本小题7分) 在同一直角坐标系中,
(1)作出函数
和
的图象.
(2)用图象求不等式
的解集.
22、(本小题7分) 已知函数
(1)若函数图象是经过原点的直线, 求的值.
(2)若这个函数是一次函数,且随着的增大而减小, 求的取值范围.
(3)若这个函数是一次函数,且图象不经过第四象限, 求的取值范围.
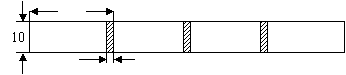
23、(本小题6分)将长为30cm，宽为10cm的长方形白纸，按如图所示的粘合起来，粘合部分的宽为3cm.设x张白纸粘合后的总长度为ycm,
（1）写出y与x的函数关系式.
（2）当x=20时, 求y的值.
24、(本小题8分)为了保护学生的视力，课桌的高度ycm与椅子的高度xcm(不含靠背)都是按y是x的一次函数关系配套设计的，下表列出了两套课桌椅的高度：
(1)请确定)y与x的函数关系式
(2)现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套?请通过计算说明理由。
| 第一套 | 第二套 | |
| 椅子高度xcm | 40.0 | 37.0 |
| 课桌高度ycm | 75.0 | 70.2 |
25、(本小题10分)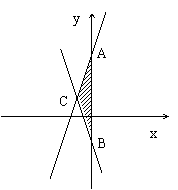
.已知，直线y=2x+3与直线y=-2x-1.
（1）求两直线与y轴交点A，B的坐标;
（2）求两直线交点C的坐标;
（3）求△ABC的面积.
26、(本小题10分) 某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测：服药后每毫升血液中含药量y与时间t之间关系如图所示:
(1)分别求出
和
时,y与t之间的函
数关系式；
(2)据测定：每毫升血液中含药量不少于4微克
时治疗疾病有效,假如某病人一天中第一次服药
为7:00,那么服药后几点到几点有效?
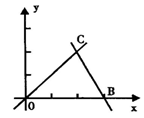
27、(本小题12分)如图，直线OC、BC的函数关系式分别是y1=x和y2=-2x+6，动点P（x，0）在OB上运动（0<x<3），过点P作直线m与x轴垂直．
（1）求出点C的坐标，并回答当x取何值时y1>y2
（2）设△COB中位于直线m左侧部分的面积为s，求出s与x之间函数关系
（3）当x为何值时，直线m平分△COB的面积？
