圆的适应性测试题

圆的适应性测试题（一）

（时间：120分钟　 满分：120分）

一、填空题（3分×10 = 30分）

1．在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，则⊙O的直径是　　　　；

2．已知⊙O的半径为2cm，弦AB的长为2cm，则这条弦的中点到弦所对的劣弧中点的距离是　　　　　　 ；

3．在半径为5cm的圆内有两条相互平行的弦，一条长是8cm，另一条长为6cm，则这两条弦之间的距离是　　　　　　　  ；

⌒

⌒

4．已知：⊙O的半径OA = 1，弦AB、AC的长分别是，则∠BAC的度数是　　；

⌒

⌒

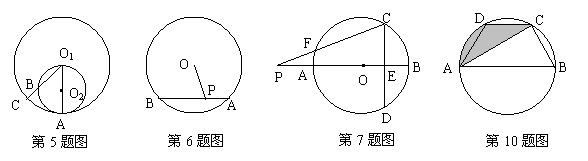5．如图，大圆O₁的半径O₁A是小圆O₂的直径，⊙O₁的半径O₁C交⊙O₂于点B，则AB与AC的长度的大小关系是AB　　 AC。（填：“＞”、“＜”或“=”

6．如图，AB是⊙O的弦，P是AB上一点，AB = 10cm，PA = 4cm，OP = 5cm，则⊙O的半径是　　　　　　 cm；

7．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，P是BA延长线上的点，连结PC，交⊙O于F，如果PF = 7，FC = 13，且PA∶AE∶EB = 2∶4∶1，则CD的长是　　　　 ；

8．已知正六边形的边心距是，则这个正六边形的周长是　　　　　　  ；

9．同一个圆的外切正三角形与内接正三角形的面积之比是　　　　　  ；

10．如图，已知⊙O的内接等腰梯形ABCD的下底AB恰为⊙O的直径，∠CAD = 15°，若⊙O的半径为R，则图中阴影部分的面积等于　　　　　　　　  ；

⌒

二、选择题（3分×6 = 18分）

11．如图，A、B、C是⊙O上的三点，AB的度数是50°，∠OBC = 40°，则∠OAC =（　 ）

　　　 A．15°　　　　B．25°　　　　 C．30°　　　　D．40°

12．如图，四边形ABCD是⊙O的内接四边形，AD为⊙O的直径，若∠CBE = 50°，则圆心角∠AOC等于（　　）

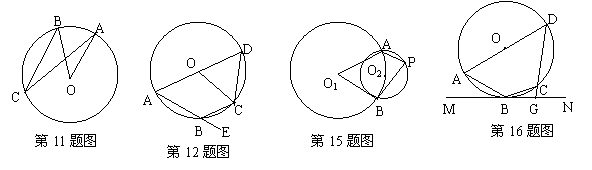　　　 A．50°　　　　B．80°　　　　 C．100°　　　 D．130°

13．若已知两圆有且只有三条公切线，则这两圆的位置关系是（　　 ）

　　　 A．外离　　　　B．外切　　　　 C．内切　　　　D．相交

14．已知两圆的圆心距是5，两圆的半径是方程x ²　7x + 10 = 0的两根，则这两圆的位置关系是（　　 ）

　　　 A．外离　　　　B．外切　　　　 C．内切　　　　D．内含

15．如图，⊙O₁和⊙O₂相交于点A、B，且⊙O₂的圆心在⊙O₁上，P是⊙O₂上一点，已知∠AO₁B = 60°，则∠APB的度数是（　　）

A．60°　　　　B．65°　　　　 C．70°　　　　D．75°

16．如图，已知四边形ABCD为圆内接四边形，AD为圆的直径，直线MN切圆于B，DC的延长线交MN于G，若cos∠ABM = ，则tan∠BCG的值为（　　）

　　　 A．　　　　 B．　　　　　C．1　　　 D．

三、解答题

17．（6分）如图，已知AC切⊙O于C点，CP为⊙O的直径，AB切⊙O于D与CP的延长线交于B点，若AC = PC。求证：（1）BD = 2BP；（2）PC = 3BP；

⌒

⌒

18．（12分）如图，已知⊙O₁与⊙O₂相交于点C、D，A是⊙O₁上一点，直线AD交⊙O₂于点B。（1）当点A在CAD上运动到A′点时，作直线A′D交⊙O₂于点B′，连A′C、B′C，证明：△A′B′C≌△ABC；（2）问点A′在CAD上什么位置时，S_△A′B′C最大，请说明理由；（3）当O₁O₂ = 11，CD = 9时，求S_△A′B′C的最大值；

19．（7分）如图，已知菱形ABCD的对角线AC、BD相交于点O，⊙O′是△ABD的外接圆，E是⊙O′上一点，连结AE并延长与BD的延长线相交于点F。求证：AC ² + BD ² = 4AE·AF；

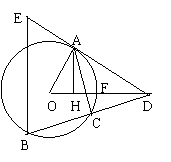20．（10分）如图，已知割线DCB交⊙O于点C、B，DA切⊙O于点A，BE // CA，交DA于点E，OD交⊙O于点F，AH⊥OD，垂足为H，且OH∶HF = 2∶3，FD = 9，AE = 2，求cos∠ODB的值；

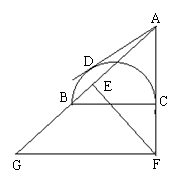21．（7分）如图，已知BC为半圆的直径，AD与半圆相切于点D，在AB上截取AE = AD，过E作EF⊥AB，交AC的延长线于点F，过F作GF // BC，交AB的延长线于点G。求证：（1）AE·AB = AC·AF；（2）AB ² = AD·AG；

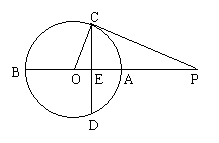22．（10分）AB是⊙O的直径，点P在BA的延长先上，弦CD⊥AB，垂足为E，∠POC=∠PCE，（1）求证：PC是⊙O的切线；（2）若OE∶EA = 1∶2，PA = 6，求⊙O的半径；（3）求sin∠PCA的值；

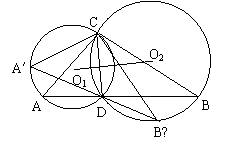
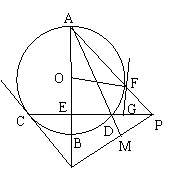23．（10分）如图，已知AB、CD是⊙O的两条互相垂直的弦，E为垂足，P是CD延长线上的一点，PA交⊙O于F，GF求⊙O与F且与CP交于G，CH切⊙O于C且与AB的延长线交于H，如果GP ² = GD·GC，AD平分∠BAP并交HP于M。求证：（1）AB为⊙O的直径；（2）MH = MP；（3）；

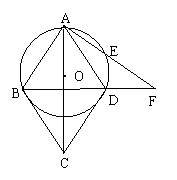
24．（10分）如图，△ABC内接于⊙O，∠BAC的平分线交⊙O于点D，交⊙O的切线BF于点F，B为切点。求证：（1）BD平分∠CBF；（2）AB·BF = AF·CD。