线段比例关系的证明问题

（二）线段比例关系的证明问题

⌒

⌒

【例1】（盐城市，1997）如图，两圆内切于T，大圆的弦AB切小圆于C，TA、TB与小圆分别相交于E、F，FE的延长线交两圆的公切线TP于点P。求证：（1）CE = CF；（2）AC·PF = BC·PT；

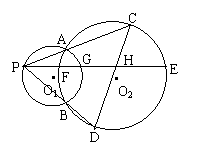
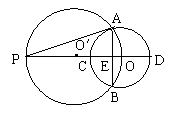【例2】（宿千市，1999）如图，⊙O和⊙O′相交于A、B，且⊙O′过⊙O的圆心。直线OO′交⊙O于C、D两点，交⊙O′于P点，AB与OO′交于E点。求证：（1）PA ² = PE·PO；（2）PE·EO = CE·ED；（3）；

【例3】（深圳市，1999）如图，⊙O和⊙O′外切于P，两圆的外公切线切⊙O于点M、切⊙O′于点N，A为切线外一点，AM、AN的延长线分别交⊙O于点B，交⊙O′于点C。

求证：（1）∠MPN = 90°；（2）当∠A = 90°时，B、P、C为一直线；（3）若PD⊥MN，垂足为D，⊙O的半径为R，⊙O′的半径为r，则

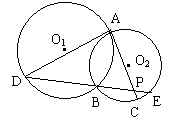
【例4】（青岛市，2001）已知：如图，⊙O₁与⊙O₂外切于点P，AB为⊙O₁、⊙O₂的外公切线，切点分别为A、B，连心线O₁O₂分别交⊙O₁于D，交AB于C。连结AD、AP、BP。

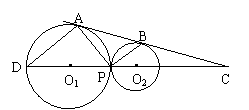求证：（1）AD // BP；（2）CPCO₁ = CDCO₂；（3）；

【热点考题训练】

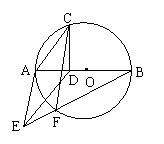
1、（四川省，2001）已知：如图，AB为⊙O的直径，AC为弦，CD⊥AB于D，若AE = AC，BE交⊙O于点F，连CF、DE。求证：（1）AE ² = AD·AB；（2）∠ACF =∠AED。

⌒

⌒

⌒

2、（哈尔滨市，2001）已知：如图，CD是△ABC外角∠MCA的平分线，CD与三角形的外接圆交于点D。（1）若∠BCA = 60°，求证：△ABD为等边三角形；（2）设点F为AD上一点，且AF = BC，DF的延长线交BA的延长线于电E。求证：AC·AF = DF·FE。

3、（新疆维吾尔族自治区，1997）已知：如图，⊙O₁与⊙O₂相交于点A、B，点O₂在⊙O₁上，AD是⊙O₂的直径，连结DB并延长交⊙O₁于点C。求证：；

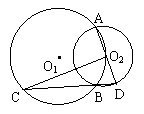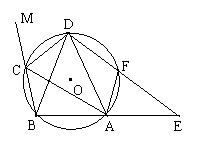
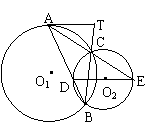4、（连云港市，1997）如图，已知⊙O₁与⊙O₂相交于点B和点C，A是⊙O₁上的另一点，AB与AC的延长线分别交⊙O₂于点D和E，如果CB与DE相交于点F。过点A的⊙O₁的切线与BC的延长线交于点T。求证：；

	F

5、（扬州市，1997）如图，以O为圆心的两个圆中，大圆的弦AB与小圆相切于C，AD与小圆相切与D，DC的延长线与大圆相交于E。求证：（1）∠ABE =∠AED；（2）AD ² = EC·ED；（3）AB = AE；

6、（黄冈市，1996）如图，⊙O₂经过⊙O₁的圆心O₁且与⊙O₂相交于点A和B，AC为⊙O₁的直径，直线CB交⊙O₂于D，AD交⊙O₁于E，BE的延长线交⊙O₂于F，连结AF、FD。

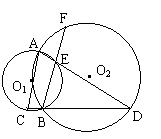求证：（1）DA = DC；（2）⊙O₁与⊙O₂的周长之比等于AE∶AF；

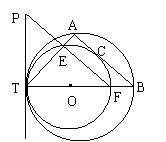
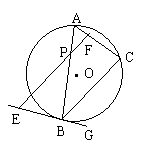
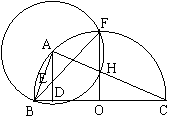7、（黄冈市，1998）如图，⊙O是△ABC的外接圆，BC是直径，以顶点A为圆心，AB长为半径的圆交⊙O于F点，交B于G点（AB＜OB），AD⊥BC于D，AD与BF交于E点，OF交⊙A于H点。求证：（1）△ABE是等腰三角形；（2）；

8、（四川省南充市，2001）已知：如图，⊙O是△ABC的外接圆，∠BAC的平分线交BC于点E，交⊙O于点D，CF // BD，交AD于点F，过点C作AD的垂线交AD于点G，交AB于点K。

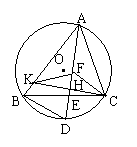求证：（1）FK = FC；（2）AB·FK = AD·CE；

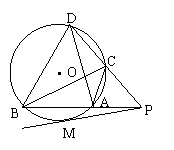9、（福州市，1997）如图，PM是⊙O的切线，M为切点，PAB和PCD均是⊙O的割线，它们与⊙O的交点分别为A、B、C、D，且AB·PD = BC·AD。求证：（1）∠DAP =∠BAC；（2）△PAC∽△DAB；（3）PM ² – PA ² = AC·AD；

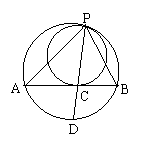10、（天津市，2000）如图，两圆内切于P，大圆的弦AB切小圆于点C。PC的延长线交大圆于点D。求证：（1）∠APD =∠BPD；（2）PA·PB = PC ² + AC·CB；

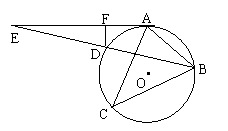11、（宁夏自治区，1997）如图，△ABC内接于⊙O，AE切⊙O于A，BD平分∠ABC交⊙O于D，交AE于E，DF⊥AE于F。求证：（1）；（2）AC = 2AF；

12、（贵阳市，2001）已知：如图，⊙O₂过⊙O₁的圆心O₁，且与⊙O₁内切于点P，弦AB切⊙O₂于点C，PA、PB分别与⊙O₂交于D、E，延长PC交⊙O₁于点F，连结CD、CE、AF。

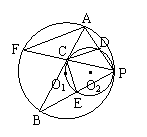求证：（1）PF平分∠APB；（2）CP ² = 2PD·EP；

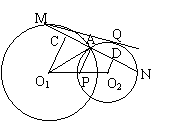13、（扬州市，1999）如图，A是⊙O₁与⊙O₂的一个交点，点P是O₁O₂的中点，过点A的直线MN垂直于PA，分别交⊙O₁、⊙O₂于M、N，O₁C、O₂D均垂直于MN，C、D为垂足，MQ是⊙O₂的切线，Q为切点。（1）求证：① MA = AN；② MQ ² = 2CD ²；（2）若直线O₁A与⊙O₂相切，求证：MQ ² = 8O₁C·O₂D；

14、（山西省，2000）如图，⊙O₁与⊙O₂相交于A、B，P是⊙O₁上的一点，连结PA、PB并延长，分别交⊙O₂于C、D，点E是CD上的任意一点，PE分别交⊙O₂、⊙O₁、CD于F、G、H。

求证：PF·PE = PG·PH；

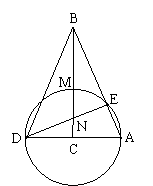15、（江西省，2000）如图，在△ABC中，∠ACB = 90°，以C为圆心，CA的长为半径的圆分别交AB、CB于E、M，AC的延长线交⊙C于D，连结DE交CB于N，连结BD。求证：（1）△ABD是等腰三角形；（2）CM ² = CN·CB；

16、（广东省，2000）如图，AB是⊙O的直径，点C在⊙O上，过O作ED // CB交AC于F，使EF = CB，连AF并延长交⊙O于G，交CB的延长线于D。连BE，并延长交⊙O于H。

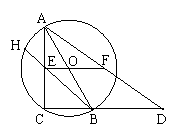求证：（1）AG = HB；（2）AE ² = HE·FD；

	G

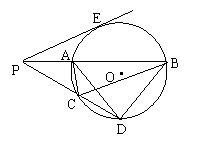
17、（聊城市，1999）如图，⊙O的割线PAB、PCD分别与⊙O交于A、B、C、D，且ADBC = CDPB。（1）求证：∠ACP = ∠BCD；（2）若PE是⊙O的切线，E为切点。求证：；

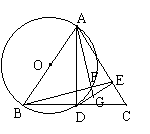18、（泰州市，1999）如图，在等腰△ABC中，AB = AC，以AB为直径的⊙O交BC于D，过D作DE⊥AC于E，BE交⊙O于F，AF的延长线交DE于G。求证：（1）DE是⊙O的切线；（2）△ADG∽△BCE；（3）EF·EB = 4GF·GA；

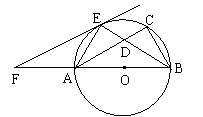19、（天门市，2000）如图，以Rt△ABC的斜边AB为直径作△ABC的外接圆O，∠B的平分线BE交AC于D，交⊙O于E，过E作EF // AC交BA的延长线于F。（1）求证：EF是⊙O的切线；（2）求证：AE ² = CDEF；（3）若AB = 15，EF = 10，求DC的长；

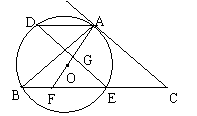20、（贵阳市，1999）如图，AC切⊙O于点A，AB为⊙O的弦，AB = AC，BC交⊙O于E，⊙O的弦AD // BC，AO的延长线交BE于F。求证：（1）四边形ADEC是平行四边形；（2）EG ² = CF·CB；

二、圆的计算问题

⌒

线段的计算问题

【例1】（黄冈市，1999）如图，⊙O是以AB为直径的△ABC的外接圆，D是劣弧BC的中点，连AD并用处与过C点的切线交于P，OD与BC相交于E。（1）求证：OE = AC；（2）求证：；（3）当AC = 6，AB = 10时，求切线PC的长；

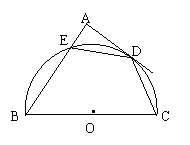
【例2】（孝感市，2000）如图，BC为半圆的直径，O为圆心，BC = 10，AD与半圆相切于D，DA⊥AB，AD = 4。（1）试求BE的长；（2）求tg∠AED的值；（3）求证：CD = DE；

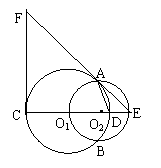
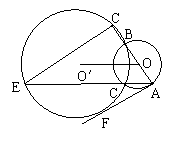
【例3】（宿迁市，2001）已知：如图，⊙O₁与⊙O₂相交于点A、B且点O₁在⊙O₂上，直线O₁O₂交⊙O₁于点C、D，交⊙O₂与点E，过点C作CF⊥CE，交EA的延长线与点F，若DE = 2，AE = 2。（1）求证：EF是⊙O₁的切线；（2）求线段CF的长；（3）求tan∠DAE的值；

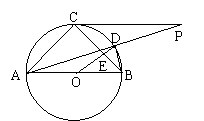
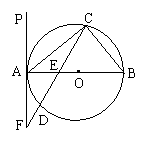
【例4】（北京市海淀区，2001）如图，△ABC内接于⊙O，AB是⊙O的直径，PA是过A点的直线，∠PAC =∠B。（1）求证：PA是⊙O的切线；（2）如果弦CD交AB于E，CD的延长线交PA于F，AC = 8，CE∶ED = 6∶5，AE∶EB = 2∶3，求AB的长和∠ECB的正切值；

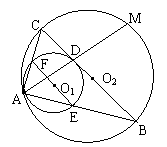【例5】（辽宁省，1999）如图，⊙O₁和⊙O₂内切于A，⊙O₂的弦BC切⊙O₁于D，AD的延长线交⊙O₂于M，连AB、AC分别交⊙O₁于E、F，连EF。（1）求证：EF // BC；（2）求证：AB·AC = AD·AM；（3）若⊙O₁的半径R₁ = 3，⊙O₂的半径R₂ = 8，BC是⊙O₂的直径，求AB和AC的长（AB＞AC）；

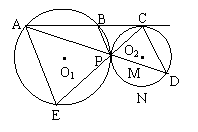
【例6】（随州市、仙桃市，2000）如图，⊙O₁和⊙O₂外切于点P，A是⊙O₁上一点，AC切⊙O₂于点C，交⊙O₁于点B， AP的延长线交⊙O₂于点D，CP的延长线交⊙O₁于点E，连AE、PB、CD。（1）求证：AE // CD；（2）求证：；（3）当⊙O₂的半径为，APPD = 97，tan∠CAD = 时，求切线AC的长；

【热点考题训练】

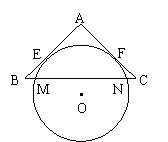1、（广东省，1997）如图，⊙O分别切AB、AC于E、F，且交BC于M、N两点，∠A = 90°，∠B =∠C，EB = 1，△ABC的面积为S₁，⊙O的面积为S₂，S₁∶S₂ = 25∶32π。（1）求证：BM = NC；（2）求BM。

	⌒		⌒

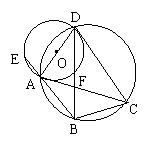2、（广西壮族自治区，1997）如图，四边形ABCD是圆内接四边形，DB = DC，以AD为直径作⊙O交BA的延长线于E，交AC、BD交于点F。（1）求证：AE = AF；（2）设AB = 2，AC = 7，求AE的长。

	⌒

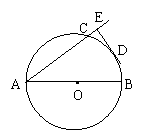3、（龙岩市、宁德市，2001）如图，已知AB、AC分别为⊙O的直径和弦，D为BC的中点，DE⊥AC于E，DE = 6cm，CE = 2cm。（1）求证：DE是⊙O的切线；（2）求弦AC的长；（3）求直径AB的长；

4、（新疆维吾尔族自治区，1999）如图，⊙O和⊙O′相交于B、C两点，AB是⊙O的直径，AC是⊙O的弦，延长AB和AC分别交⊙O′于D、E连点，连DE，AF是⊙O′的切线，F为切点。若AF = ，EC = 5，DB∶BA = 1∶2。（1）∠BAC的度数；（2）求圆心距OO′的长；

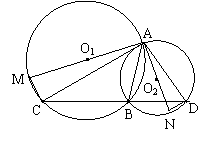5、（泉州市，1997）如图，AB为⊙O₁与⊙O₂的公共弦，经过点B的直线和两圆分别相交于点C和D，AM、AN分别为⊙O₁和⊙O₂的直径。（1）求证：△AMC∽△AND；（2）设AC∶AD = 3∶2，AM + AN = 12，试分别求两圆的直径；

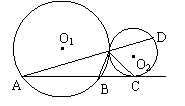
6．（南京市，1997）如图，⊙O₁与⊙O₂外切于P，A为⊙O₁上一点，直线AC切⊙O₂于点B，AP的延长线交⊙O₂于点D。（1）求证：∠BPC =∠CPD；（2）若⊙O₁的半径是⊙O₂半径的2倍，PD = 10，AB = 7，求PC的长。

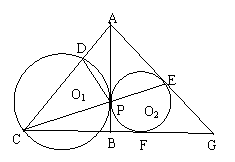7．（潜江市，2001）如图，已知⊙O₁与⊙O₂外切于P，AB是两圆的内公切线，AE切⊙O₁于E，EP的延长线交⊙O₂于C，CF切⊙O₁于F，交直线AE于G，交公切线于B，AC交⊙O₂于D，连DP。（1）求证：CP·CE = CD·CA；（2）求证：AE ² + CF ² = AC ²；（3）若AB⊥CG，⊙O₁的半径是1，EG = 3，cot∠AEP = ，求AC的长。

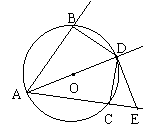8．（南通市，1997）如图，过∠BAC的顶点A作⊙O交角的两边于点B、C，⊙O交该角的平分线于点D，DE切⊙O于点D，交AC边于点E。（1）求证：BD ² = AB·CE；（2）若BD = 3，DE + CE = 12，，求DE。

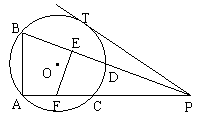9．（南通市，2000）如图，P是⊙O外一点，割线PA、PB分别与⊙O相交于A、C、B、D四点，PT切⊙O于T，点E、F分别在PB、PA上，且PE = PT，∠PFE =∠ABP。（1）求证：PD·PF = PC·PE；（2）若PD = 4，PC = 5，AF = ，求PT的长；

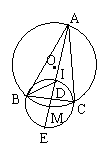10．（泰州市，1997）如图，已知M为⊙O上一点，⊙M与⊙O交于B、C两点，过M的直线交⊙O于A点，交⊙M于I和E点，连AB、AC、BI。（1）求证：BI平分∠ABC；（2）求证：ME是MD和MA的比例中项；（3）若AB = 4，AC = 3，EM = 2，求AI的长；

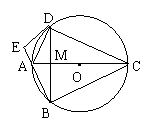11．（北京市朝阳区，2001）已知：如图，四边形ABCD内接于⊙O，AC为⊙O的直径，弦DB⊥AC，垂足为M，过点D作⊙O的切线，交BA的延长线于点E，若AC = 10，tan∠DAE = ，求DB和DE的长。

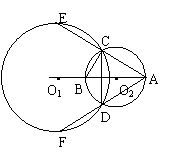12．（海南省，1998）如图，⊙O₁和⊙O₂相交于C、D两点，连心线O₁O₂和⊙O₂相交于B、A两点，AC、AD的延长线分别和⊙O₁相交于E、F。（1）求证：CE = DF；（2）如果⊙O₂的半径为2，∠ABC = 60°，且EC = CD，求⊙O₁的半径；

⌒

⌒

13．（无锡市，2001）如图，弓形AmB小于半圆，它所在圆的圆心为O，半径为13，弦AB的长为24；C是弦AB上的一动点（异于A、B），过C作AB的垂线交AB于点P，以PC为直径的圆交AP于点D，E是AP的中点，连结OE。（1）当点D、E不重合时，求证：OE // CD；（2）当点C是弦AB的中点时，求PD的长；

	⌒

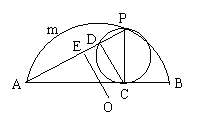
14．（咸宁地区，2000）如图，，等边△ABC内接于⊙O，D为AC上一点，CD的延长线与BA的延长线交于E。（1）求证：BC ² = CD·CE；（2）如果CD = 1，DE = 3，求AE的长；

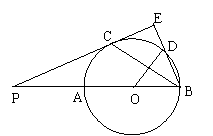15．（南充市，2001）如图，AB是⊙O的直径，延长BA到点P，PC是⊙O的切线，切点为C，过点B作PC的垂线交⊙O于点D，交PC于点E，PA = 1，PC∶OD = ∶1。求（1）BC的长；（2）CD·DE的值；

16．（北京西城区，2000）如图，△ABC是⊙O的内接三角形，BT为⊙O的切线，B为切点，P为直线AB上一点，过点P作BC的平行线交直线BT于点E，交直线AC于F。（1）点P在线段AB上时，求证：PA·PB = PE·PF；（2）当点P为线段BA延长线上一点时，第（1）题的结论还成立吗？如果成立，请证明；如果不成立，请说明理由；（3）若AB = 4，cos∠EBA = ，求⊙O的半径；

17．（黄冈市，2000）如图，⊙O₁与⊙O₂相交于A、B两点，过A作⊙O₁的切线，交⊙O₂于C，过B作两圆的割线分别交⊙O₁、⊙O₂于D、E，DE与AC相交于点P。（1）求证：PA·PE = PC·PD；（2）当AD与⊙O₂相切，且PA = 6，PC = 2，PD = 12时，求AD的长；

	⌒

18．（北京石景山区，2000）AD是⊙O的直径，且AD = 2，C是AD的中点。若B为⊙O上一点，且AB = ，求以A、B、C、D为顶点的四边形的周长。

三、其他计算问题（角、弧长、面积等）

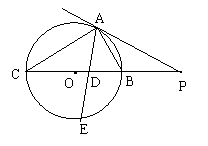1．（辽宁省，1997）如图，PA为⊙O的切线，A为切点，PBC是过O的割线，PA = 10，PB = 5，∠BAC的平分线与BC和⊙O分别相交于点D和E。求（1）⊙O的半径；（2）sin∠BAP的值；（3）AD·AE的值；

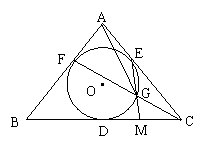2．（武汉市，1998）如图，已知在△ABC中，AB = AC，且⊙O内切于△ABC，D、E、F是切点，又CF交圆于G，EG的延长线交BC于M，AG交圆于K。（1）求证：△MCG∽△MEC；（2）若EM⊥CD，求cos∠FAK的值；

3．（四川省，1999）如图，AD、BC是⊙O₁的两条弦，且AD // BC，以CD为直径的⊙O₂交BC于E，AB = 6cm，BC = 14cm，S_△BCD = 21cm ²。求（1）EC的长；（2）弓形EmC（阴影部分）的面积（不取近似值）；

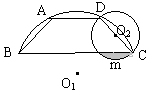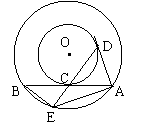
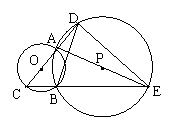4．（西藏自治区，1998）已知：如图，A、B是⊙O和⊙P的交点，AC是⊙O的直径，D、E分别是CA、CB的延长线与⊙P的交点，AC = 2，BC = AD = 1。（1）求∠C的度数；（2）求CE的长；（3）求证：BD = ；

5．（江西省，1997）如图，在△ABC中，∠B = 90°，O是AB上的一点，以O为圆心，OB为半径的圆与AB交于E，与AC切于点D，直线ED交BC的延长线于F。（1）求证：BC = FC；（2）若AD∶AE = 2∶1，求cot∠F的值；

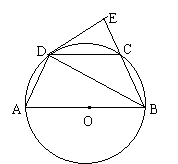6．（北京市海淀区，1997）如图，，四边形ABCD内接于半⊙O，AB为直径，过点D的切线交BC的延长线于点E，若BE⊥DE，AD + DC = 40，⊙O的半径为，求BC的长及tan∠CDB的值；

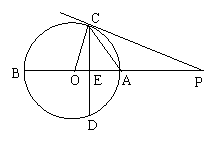7．（广西壮族自治区，1999）如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB，垂足为E，∠POC =∠PCE。（1）求证：PC是⊙O的切线；（2）若OE∶EA = 1∶2，PA = 6，求⊙O的半径；（3）求sin∠PCA的值；

	⌒

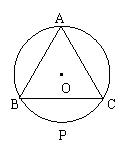
8．（广州市，1999）如图，等边三角形ABC的面积为S，⊙O是它的外接圆，点P是BC的中点。（1）试判断过点C所作⊙O的切线与直线AB是否相交，并证明你的结论。（2）设直线CP与AB相交于点D，过点B作BE⊥CD，垂足为E。证明：BE是⊙O的切线，并求△BDE的面积；

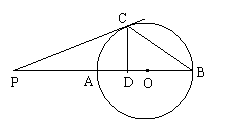9．（北京市海淀区，2000）如图，PC为⊙O是切线，PAB是过O点的割线，CD⊥AB于D。若tanB=，PC = 10cm，求△BCD的面积。

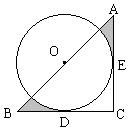10．（宁夏自治区，1999）如图，已知△ABC中，∠C = 90°，O是AB上一点，⊙O切BC于D，切AC于E，AC = b，BC = a。（1）求⊙O的半径R；（2）用a、b表示阴影部分的面积S（结果可不化简）；

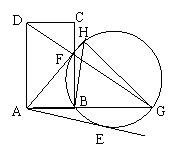11．（福州市，2000）如图，由矩形ABCD的顶点D引一条直线分别交BC及AB的延长线于F、G，连AF并延长交△BGF的外接圆于H，连GH、BH。（1）求证：△DFA∽△HBG；（2）过A点引圆的切线AE，E为切点，AE = 3，CF∶FB = 1∶2，求AB的长；（3）在（2）的条件下，又知AD = 6，求tan∠HBG的值；

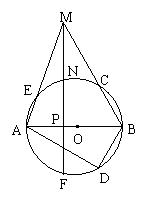
12．（北京市，2000）已知，如图，有△ABM，以AB为直径的⊙O交AM于点E，交BM于C。MP⊥AB于P，交⊙O于N、F。在AFB上取一点D，使BD = BC，AP = 1，PB = 3，S_△ABDS_△ABM = 13。求（1）线段AE的长；（2）弓形AFD的面积；

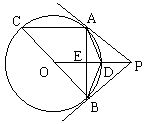
13．（宜昌市，2000）如图，P为⊙O外一点，PA、PB为⊙O的切线，A、B为切点，OP与⊙O交于D，BC是直径，四边形ACOD的面积是△BAD的面积的2倍。请回答：四边形BPAC和⊙O的面积哪一个大？请说明你的理由；

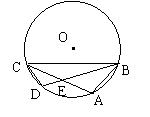14．（黑龙江省，2000）如图，已知四边形ABCD外接⊙O的半径为5，对角线AC与BD的交点为，且AB ² = AE·AC，BD = 8，求△ABD的面积。