福州十六中八年级下学期数学第六章证明（一）单元测试卷
命题人：段振富
班级 座号 姓名 成绩
一、填空题（每空3分，共 42分）
1、“两直线平行，同位角互补”是 命题（填真、假）
2、把命题“对顶角相等”改写成“如果…那么…”的形式
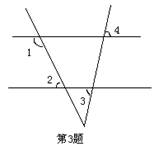
3、如图所示，∠1+ ∠2=180°，若∠3=50°，则∠4=
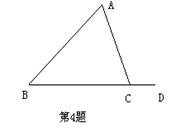
4、如图所示，△ABC中，∠ACD=115°，∠B=55°,则∠A= , ∠ACB=
5、在△ABC中，∠C=90°，若∠A=30°，则∠B=
6、在△ABC中，∠B—∠C=40°，则∠C= ，∠B=
7、在三角形中，最多有 个锐角，至少有 个锐角，最多有 个钝角（或直角）
8、△ABC的三个外角度数比为3∶4∶5，则它的三个外角度数分别为
9、在△ABC中，∠ABC和∠ACB的平分线交于点I, 若∠A=60°，则∠BIC=
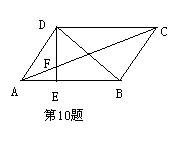
10、已知如图，平行四边形ABCD中，E为AB上一点，DE与AC交于点F，AF∶FC=3∶7，则AE∶EB=
二、选择题（每小题3分，共18分）
11、下列命题是真命题的是（ ）
A、同旁内角互补
B、直角三角形的两锐角互余
C、 三角形的一个外角等于它的两个内角之和
D、三角形的一个外角大于内角
12、下列语句为命题的是（ ）
A 、你吃过午饭了吗？ B、过点A作直线MN
C、同角的余角相等 D、红扑扑的脸蛋
13、命题“垂直与同一条直线的两条直线互相平行”的题设是（ ）
A、垂直 B、两条直线 C、同一条直线 D、两条直线垂直于同一条直线
14、已知△ABC的三个内角度数比为2∶3∶4，则个三角形是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形
15、如图，一个任意的五角星，它的五个内角的度数和为（ ）
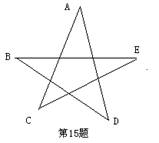A、90°
B、180°
C、360°
D、120°
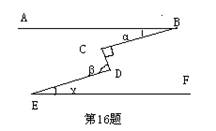
16、如图，AB∥EF， ∠C=90°，则α、β、γ的关系为（ ）
A、β=α+γ B、α+β+γ=180° C、β+γ-α=90° D、α+β-γ=90°
三、完型填空（每空2分，共8分）
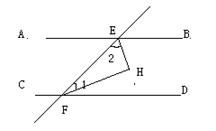
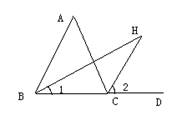17、已知如图，在△ABC中，CH是外角∠ACD的平分线，BH是∠ABC的平分线。
求证：∠A= 2∠H
证明： ∵∠ACD是△ABC的一个外角，
∴∠ACD=∠ABC+∠A （ ）
∠2是△BCD的一个外角，
∠2=∠1+∠H ( )
∵CH是外角∠ACD的平分线，BH是∠ABC的平分线
∴∠1= 
∠ABC ，∠2= ∠ACD （
）
∴∠A =∠ACD-∠ABC= 2 （∠2 - ∠1） （等式的性质）
而 ∠H=∠2 - ∠1 （等式的性质）
∴∠A= 2∠H （ ）
四、解答题（每题8分，共 32分）
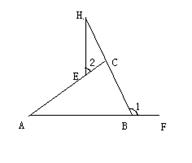
18、已知如图，在△ABC中，∠1是它的一个外角，E为边AC上一点，延长BC到D，连接DE。
求证：∠1 > ∠2
19、求证：两条直线平行，同旁内角的角平分线互相垂直。
（提示：先画图，写出已知，求证，然后进行证明）
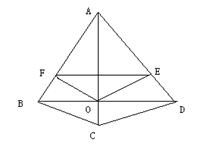
19、已知如图，O是四边形ABCD的两条对角线的交点，过点O作OE∥CD，交AD于E，作OF∥ BC，交AB于F，连接EF。
求证：EF∥BD
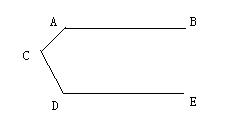
20、已知如图，AB∥DE。（1）、猜测∠A、∠ACD、∠D有什么关系，并证明你的结论。
（2）、若点C向右移动到线段AD的右侧，此时∠A、∠ACD、∠D之间的关系，仍然满足（1）中的结论吗？若符合请你证明，若不符，请你写出正确的结论并证明。要求画出相应的图形。
