求代数式的值
阆中市千佛镇中：赵武成
求代数式的值涉及的问题较多，包括整式求值、分式求值、根式求值。具有很强的综合性，要用到许多的数学思想和方法，具有很强的灵活性。
一、直接公共秩序求值：
例1、已知x=－3，y=2，求x2y+x－y的值。
二、化简代数式再公共秩序求值：
例2、已知a=－3，b=2，求
的值。
三、整体代入法（联系配方思想转化）：
例3、已知x+y=－4，xy＝－12，求
的值。
解：
（以下略），再代入（x+y）与xy即可求得。
四、利用非负数的性质求值。
若A2＋
＝0，则A＝0，B＝0，C＝0。
例4、已知
，求a3－b3的值。
解：由题意得
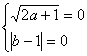
解得：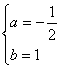
∴a3－b3＝
＝
五、换元、消元法
例5、已知
，求
的值。
解：由得
把代入原式得（以下略）
例6、已知
，求
的值。（解略）
例7、已知4x－3y－6z=0，x+2y－7z＝0（z≠0），求
的值。
分析：三个未知数，两个方程，不能直接求得未知数的值。可以考虑用含某一个未知数的式子换另两个未知数。
解：由
得
∴
（以下略）
六、配方法（配成完全平方式：加上一次项系数一半的平方）：
例8、a+b=3，ab=－2，求a2+b2与
的值。（解略）
例9、已知a2+b2－10a－6b＋34＝0，求
的值。（提示：利用非负数性质）
七、设辅助未知数法（又称参数法、待定系数法。类似于换元法）：
例10、已知：
，求
的值。
解：设
，则x=5m，y=3m。
∴原式＝
（以下略）
八、分解法：
例11、已知x+3y=5,2x－y=0.5，求2x2+5xy－3y2的值。（解略）
九、利用定义法：即直接代入求值。（略）
十、综合各种方法：
例12、已知3a2+ab－2b2＝0，求
的值。（提示：可考虑将已知部分分解，将求值部分化简再代入）
练习：
1、已知a+b=－3，ab=2，求a2b2－a2－b2－4ab+1的值。
2、已知a2+b2－2b-6b+10=0，求
的值。
3、已知
，求
的值。
4、若
，求的值。