三、不等式
考试内容：
不等式.不等式的性质.不等式的证明.不等式的解法.含有绝对值的不等式.
考试要求：
(1)掌握不等式的性质及其证明，掌握证明不等式的几种常用方法，掌握两个(或三个)正数的算术平均数不小于它们的几何平均数这一定理，并能运用上述性质、定理和方法解决一些问题.
(2)在熟练掌握一元一次不等式(组)、一元二次不等式的解法的基础上初步掌握其他的一些简单的不等式的解法.
(3)会用不等式a－b≤a＋b≤a＋b解一些简单问题.
一、选择题
1. (87(3)3分)设a，b是满足ab＜0，的实数，那么
A.a＋b＞a－b B.a＋b＜a－b C.a－b＜a－b D.a－b＞a＋b
2. (90(12)3分)已知h＞0设命题甲为:两个实数a，b满足a－b＜2h；命题乙为:两个实数a，b满足a－1＜h且b－1＜h，那么
A.甲是乙的充分条件，但不是乙的必要条件
B.甲是乙的必要条件，但不是乙的充分条件
C.甲是乙的充要条件
D.甲不是乙的充分条件，也不是乙的必要条件.
3. (90上海)若函数f(x)、g(x)的定义域和值域都为R，则f(x)＞g(x)(x∈R)成立的充要条件是
A.有一个x∈R，使得f(x)＞g(x) B.有无穷多个x∈R，使得f(x)＞g(x)
C.对R中任意的x，都有f(x)＞g(x)＋1 D.R中不存在x，使得f(x)≤g(x)
4. (90上海)不等式
－3＜1的解集是
A.{x5＜x＜16} B.{x6＜x＜18} C.{x7＜x＜20} D.{x8＜x＜22}
5. (90广东)如果x，y是实数，那么“xy＞0”是“x＋y＝x＋y”的
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分又不必要条件
6. 若loga2＜logb2＜0，则(92(7)3分)
A.0＜a＜b＜1 B.0＜b＜a＜1 C.a＞b＞1 D.b＞a＞1
7. (93(10)3分)若a，b是任意实数，且a＞b，则
A.a2＞b2 B.
＜1 C.lg(a－b)＞0 D.
8. (93上海) “a＋b＞2c”的一个充分条件是
A.a＞c或b＞c B.a＞c且b＜c C.a＞c且b＞c D.a＞c或b＜c
9. (94上海)若0＜a＜1，则下列不等式中正确的是
A.(1－a)
＞(1－a)
B.log(1－a)(1＋a)＞0 C.(1－a)3＞(1＋a)2 D.(1－a)1＋a＞1
10. (95上海)当0＜a＜b＜1时，下列不等式正确的是
A.(1－a)
＞(1－a)b
B.(1＋a)a＞(1＋b)b
C.(1－a)b＞(1－a)
D.(1－a)a＞(1－a)b
11.(97(14)5分)不等式组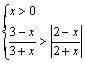
的解集是
A.{x0＜x＜2} B.{x0＜x＜2.5} C.{x0＜x＜
} D.{x0＜x＜3}
12.(2000⑺5分)若a＞b＞1，P＝
，Q＝
(lga＋lgb)，R＝lg(
)，则
A.R＜P＜Q B.P＜Q＜R C.Q＜P＜R D.P＜R＜Q
13.(2001(1)5分)若
＞0，则
在
A．第一、二象限 B．第一、三象限 C．第一、四象限 D．第二、四象限
15.(2001上海(13)4分)若
、
为实数，则
是
的（ ）
A．充分不必要条件． B.必要不充分条件．
C．充要条件． D．既非充分条件也非必要条件．
二、填空题
1. (89(14)4分)不等式x2－3x＞4的解集是______________.
2. (91(17)3分)不等式6x2＋x－2＜1的解集是______________.
3. (93(22)3分)建造一个容积为8m2，深为2m的长方体无盖水池，如果水池底和池壁的造价每平方米分别为120元和80元，那么水池的最低总造价为__________元.
4. (94上海)不等式x＋1＜1的解集是____________
5. (95(16)4分)不等式
的解集为______________.
6. (95上海)不等式
＞1的解集为______________.
7. (99(17)4分)若正数a、b满足ab＝a＋b＋3，则ab的取值范围是___________
三、解答题
1. (85(12)7分)解不等式
＞x＋1.
2. (86(18)12分)当sin2x＞0时，求不等式log0.5(x2－2x－15)＞log0.5(x＋13)的解集.
3. (87(18)12分)设对所有实数x，不等式x2log2
＋2xlog2
＋log2
＞0恒成立，求a的取值范围.
4. (88(24)12分)设a＞0，a≠1，t＞0，比较logat和loga
的大小，并证明你的结论.
5. (90上海)关于实数x的不等式
x－
和x2－3(a＋1)x＋2(3a＋1)≤0(x∈R)
的解集依次为A、B，求使得A
B的a的取值范围
6. (91)设a>0,a≠1,解不等式：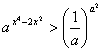
7. (91(25)12分)已知n为自然数，实数a＞1，解关于x的不等式:
logax－4log
x＋12log
x＋……＋n(－2)n－1log
x＞
loga(x2－a)
8. (91上海)解关于x的不等式(logax)2－1＞2a－1，其中a＞0，a≠1
9. (91三南)解不等式
≥x
10. (93(25)8分)解不等式:2＋log0.5(5－x)＋log2
＞0.
11. 93(29)10分)如果关于x的实系数二次方程x2＋ax＋b＝0有两个实数根α、β，证明:
Ⅰ.如果α＜2，β＜2，那么2a＜4＋b且b＜4；
Ⅱ.如果2a＜4＋b且b＜4，那么α＜2，β＜2.(
12. (96(20)11分)解关于x的不等式:loga(1－)＞1
13. (96(23)10分)某地现有耕地10000公顷，规划10年后粮食单产比现在增加22％，人 均粮食占有量比现在提高10％，如果人口年增长率为1％，那么耕地平均每年至多只能减少多少公顷(精确到1公顷)？
14. (96(25)12分)已知a、b、c是实数，函数f(x)＝ax2＋bx＋c，g(x)＝ax＋b，
当－1≤x≤1时f(x)≤1.
①证明:c≤1；②证明:当－1≤x≤1时，g(x)≤2；
③设a＞0，当－1≤x≤1时，g(x)的最大值为2，求f(x).
15. (97(22)12分)甲、乙两地相距S千米，汽车从甲地匀速行驶到乙地，速度不得超过c千米/时，已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(千米/时)的平方成正比，比例系数为b；固定部分为a元.
(Ⅰ)把全程运输成本y(元)表示为速度v(千米/时)的函数，并指出这个函数的定义域；(Ⅱ)为了使全程运输成本最小，汽车应以多大速度行驶?
16. 
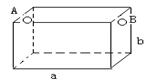(98(22)12分)如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱.污水从A孔流入，经沉淀后从B孔流出.设箱体长度为a米，高度为b米.已知流出的水中杂质的质量分数与a，b的乘积ab成反比.现有制箱材料60平方米，问当a，b各为多少米时，经沉淀后流出的水中该杂质的质量分数最小(A，B孔的面积忽略不计)
17. (99(19)10分)解不等式
＜2logax－1(a＞0，a≠1)
18. (2000安徽(23)12分)某地区上年度电价为0.8元/kw·h，年用电量为akw·h.本年度计划将电价降到0.55元/kw·h至0.75元/kw·h之间，而用户期望电价为0.4元/kWw·h.经测算，下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为K).该地区电力的成本为0.3元/kw·h.
(I)写出本年度电价下调后，电力部门的收益y与实际电价x的函数关系式；
(II)设k＝0.2a，当电价最低定为多少时仍可保证电力部门的收益比上年至少增长20%？(注：收益＝实际用电量×(实际电价－成本价))
19. (2000⒆12分)设函数f(x)＝
－ax，其中a＞0.
⑴解不等式f(x)≤1；⑵求a的取值范围，使函数f(x)在区间[0，＋∞)上是单调函数.
19.(2001(20)12分)已知i，m，n是正整数，且1＜i≤m＜n．
(Ⅰ)证明
； (Ⅱ)证明
．
20．（2001北京(17)12分）已知
为全集，
，求