81、反三角函数的概念、图象和性质
一、典型例题
1、
求函数y=2arcsin
+
的定义域和值域。
2、
求下列函数的定义域和值域：①
② y=arcos(tgx)
3、
比较下列各组数的大小：① arcsin
与arcsin
② arcctg
与arcctg
③ arccos(
)与arccos(
) ④ arctg11与arctg11.1 ⑤arcsin
与arccos
4、
若0<x<
，求arcsin[cos(+x)]+arcos[sin(p+x)]
5、
解不等式arccos(x-2)>
。
6、 已知arccos(1-x)≥arccosx，试求x的取值范围。
7、 求下列函数的反函数，并求函数的定义域和值域。
① y=tgx x∈(
) ② y=2sin2x x∈[
] ③ y=sinx (
)
8、
求函数y=-arcsinx (x∈[-1,1])的反函数。
9、 讨论函数y=arcsin(sinx)的奇偶性、周期性、单调性，并作出它在区间[-p,p]内的图象。
10、 求函数y=arcsin(x2-x)的单调区间。
11、 判断下列函数的单调性：① f(x)=tg(p-arccosx) ② F(x)=sin(arcctgx)
12、 若f(arccosx)=x2+4x，求f(x)的最小值，并求取得最小值时相应的x值。
13、 求函数y=(arcsinx)2+arcsinx-1的最大值、最小值及取得最大值、最小值时x的值。
14、
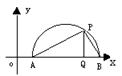
如图：设函数y=sin[arcos(x-p)]的图象与x轴相交于A、B两点，P是图象上任一点，且PQ⊥AB，垂足为Q，求∣PA∣＋∣PB∣＋∣PQ∣的最大值。