高考第一轮复习数学单元测试卷
不等式
第Ⅰ卷（选择题，共60分）
一、 选择题（本大题共12小题，每小题5分，共60分）
1、 若m<0，n>0，且m+n<0，则下列不等式中成立的是
A、-n<m<n<-m B、-n<m<-m<n C、m<-n<n<-m D、m<-n<-m<n
2、
已知
，则下列不等式中成立的是
3、 下列不等式中解集为实数集R的是
4、
5、
设
则
中最小的是
6、
不等式
的取值范围是
7、
如果方程
的两个实根一个小于-1，另一个大于1，那么实数m的取值范围是
8、
如果
的取值范围是
9、
函数
的最小值是
10、在
三个结论：①
，②
③
，其中正确的个数是
A、0 B、1 C、2 D、3
11、若不等式
内恒成立，则实数
的取值范围是
12、设
的最值情况是
A、有最大值2，最小值
B、有最大值2，最小值0
C、有最大值10，最小值
D、最值不存在
第Ⅱ卷（非选择题，共90分）
二、 填空题（本大题共4小题，每小题4分，共16分）
13、不等式
的解集为A，不等式
的解集为B，不等式
的斜率是_________。
14、如果
的解集是___________________________________________。
15、实数
_________，y=_________。
16、若
的大小关系是________________________。
三、 解答题（本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。）
17、（本小题满分10分）
，求关于
不等式
的解集。
18、（本小题满分12分）
解关于
。
19、（本小题满分12分）
已知
求证：（1）
；（2）
。
20、（本小题满分12分）
某种商品原来定价每件p元，每月将卖出n件。假若定价上涨
，每月卖出数量将减少y成，而售货金额变成原来的z倍。
（1） 若
时的
值；
（2）
若
，求使售货金额比原来有所增加的的取值范围。
21、（本小题满分14分）
已知函数
在R上是增函数，
。
（1）
求证：如果
；
（2） 判断（1）中的命题的逆命题是否成立？并证明你的结论；
（3）
解不等式
。
22、（本小题满分14分）
奇函数
上是增函数，当
时，是否存在实数m，使
对所有的
均成立？若存在，求出适合条件的所有实数m；若不存在，说明理由。
高考数学第一轮复习检测
不等式参考答案
一、 选择题：（每题5分，共60分）
1、C 2、B 3、D 4、D 5、C 6、C
7、D 8、B 9、B 10、D 11、A 12、A
二、 填空题：（每题4分，共16分
13、
14、
15、3，1，2。 16、
（用求商比较法）。
三、 解答题（共六个小题，满分74分）
17、（10分）
解集为
18、（12分）
①若
；
②若
；
③若
。
19、（12分）
证明：（1）
，
，
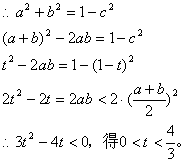
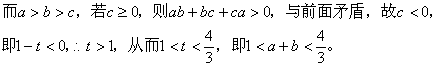
（2）首先易证
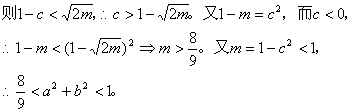
20、（12分）
解：该商品定价上涨成时，上涨后的定价、每月卖出数量、每月售货金额分别是
因而有：
（2）
21（14分）
（1）
证明：当
（2）（1）中命题的逆命题为：
①
①的逆否命题是：
②
仿（1）的证明可证②成立，又①与②互为逆否命题，故①成立，即（1）中命题的逆命题成立。
（2） 根据（2），所解不等式等价于
。
22、（14分）
解：易知
，
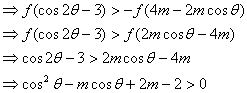
因此，满足条件的实数m存在，它可取
内的一切值。