初二几何练习
1. 已知:如图,四边形ABCD是等腰梯形,AB＝CD, AD∥BC， DE∥CA交BA的延长线于点E，
求证：ED·AB＝EA·BD
2．已知：如图，AB∥CD，AF=BF，EC=EB。
求证：OC2=OF·OD
3．已知:如图, △ABC中,BC=8cm,AB=AC=5cm, 一动点P在底边上从B向C以0.25cm/秒的速度移动,当点P运动到PA与腰垂直的位置时,求P点的运动时间t.
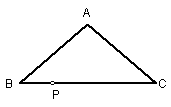
4.已知:如图,在△ABC中,AB=AC,D是BC上一点,∠BDE=∠CDF,
求证:S△BDE=S△CDE.
5.已知:如图,D为△ABC的边AC上任意一点,延长CB到E,使BE=AD,连结ED,交AB于点F,
求证:EF·BC=FD·AC.
6.已知:如图, △ABC中,AB=AC,∠A=90°,AE=
AC ,
BD=AB.
求证:∠ADE=∠EBC.
7.已知:梯形ABCD,DC∥AB,在下底AB上取AE=EF ,连结DE、CF并延长交于点G,AC与DG交于点M.
求证:DG·ME=EG·DM.
8.已知:如图,D为△ABC内一点,连结AD、BD,以BC为边,在△ABC的形外作△BCE,使
∠EBC=∠ABD,∠ECB=∠DAB.
求证:∠BDE=∠BAC.
9.已知:如图,在△ABC中, ∠ACB=90°,M是BC的中点,CN⊥AM ,垂足是N,
求证:AB·BM=AM·BN.
10.如图:在大小为4×4的正方形方格中, △ABC的顶点A、B、C在单位正方形的顶点上,请在图中画一个△A1B1C1 ,使△A1B1C1∽△ABC(相似比不为1),且点A1 、B1 、C1 都在单位正方形的顶点上.
11.已知:如图, ABCD中,线段EF∥BC,BE、CF相交于点S,AE、DF相交于点P,
求证:SP∥AB.
12.如图,在梯形ABCD中,AB∥DC,CE是∠BCD的平分线,且CE⊥AD,DE=2AE,CE把梯形分成面积为S1和S2两部分,若S1=1,求S2.
13.如图,菱形EFGH内接于 ABCD,并且EF∥AC∥HG, FG∥BD∥EH,AC=a,BD=B.
求菱形的边长.
14. 已知:如图:在△ABC中,D为AC的中点,在BC上截取BN=AB,连结AN交BD于E.
求证: 
= 
.(用多种方法证明)
15.如图:矩形ABCD中,AN⊥BD，N为垂足，NE⊥BC，NF⊥CD，垂足分别为E、F.
求证:AN3=BD·BE·DF.
