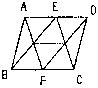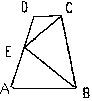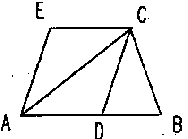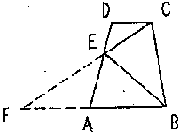初二几何--四边形练习题及答案

初二几何---四边形

一.选择题 (本大题共 20 分)

1. 梯形中位线长15cm，一条对角线把中位线分成两线段之比为2:3，则此梯形的两底长分别是（　　）
(A)14cm，16cm　　  (B)12cm，18cm　 　 (C)12cm，20cm　 　 (D)8cm，22cm

2. 下列说法不正确的是（　 ）
(A)正方形的对角线互相垂直且相等　　
(B) 对角线相等的菱形是正方形
(C)邻边相等的矩形是正方形
(D)有一个角是直角的平行四边形是正方形 

3. 菱形具有而平行四边形不具有的性质是（　 ）
(A)对角线互相平分　　 (B)邻角互补　 　(C)每条对角线平分一组对角　 　(D)对角相等

4. 有两个角相等的梯形一定是（　　）
(A)等腰梯形　　 (B)直角梯形　　 (C)等腰梯形或直角梯形　　 (D)以上都不对

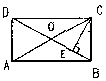
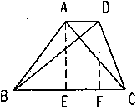
5. 如图已知：矩形ABCD中，CE⊥BD于E，∠DCE:∠ECB=3:1，则∠ACE=（　 ）
(A)30°　　 (B)45°　　(C)60°　  (D)40°

6. 下列图形中既是轴对称图形，又是中心对称图形的是（　 ）
(A)平行四边形　　 (B)等腰直角三角形　　(C)等边三角形　　(D)菱形

7. 下列语句中不一定正确的是（　　）
(A)对角线相等的梯形是等腰梯形　　 
(B)梯形最多有两个内角是直角
(C)梯形的一组对角不能相等
(D)一组对边平行的四边形是梯形

8. 如图，E、F是□ABCD两对边的中点，则图中平行四边形的个数是（　 ）
(A)4　　 (B)6　 　(C)7　   (D)8

9. 下列说法正确的是（　 ）
(A)对角相等的四边形是矩形　　 
(B)有一个角是直角的四边形是矩形　  
(C)对角互补的平行四边形是矩形
(D)三个角相等的四边形是矩形

10. 顺次连结下列四边形各边中点所得的四边形是矩形的是（　　）
(A)等腰梯形　　 (B)矩形　 　 (C)平行四边形　 　 (D)菱形

二.填空题 (本大题共 30 分)

1. 直角梯形一内角为120°，它的高与上底长都是√3cm，则它的腰长　　　cm、　　　cm，为中位线长　　　cm。

2. □ABCD的周长为56cm，对角线AC、BD交于O，ΔABO与ΔBCO的周长之差4cm，则AD=　　 cm。

3. 对角线　　　 的四边形是矩形。　 对角线　　　 的四边形是菱形。

4. 在□ABCD中，AB=6cm，BC=10cm，∠B=30°，则S_□ABCD=　　 cm。

5. 若梯形的上底长为6cm，中位线长8cm，则此梯形的下底线长　　　cm；连结两条对角线的中点的线段长　　　cm。

6. 平行四边形一边长为10，一条对角线长12，则它的另一条对角线的取值范围是　　 。

7. 等腰梯形的一条对角线分中位线为4cm和10cm两部分，腰长为12cm，则此梯形不在同一底的两内角为　　度、　　度，其面积为　　cm²。

8. 顺次连结四边形各中点所得的四边形是　　　　  形。如果新四边形的两邻边分别长3cm、4cm，那么原四边形的两条对角线之和为　　　cm。

9. 梯形一腰长4cm，这腰和底所成的角是30°，则另一腰长为　　cm。

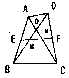
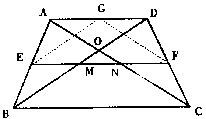
10. 如图已知：四边形ABCD中，AC、BD交于O，AC=BD，E、F为AB、CD中点，EF交BD、AC于MN。
　　求证：OM=ON

11. 对角线　　　 的四边形是矩形。　 对角线　　　 的四边形是菱形。

12. 矩形ABCD中，对角线交于O，∠AOD=120°，AB=4cm，则AD=　　 cm。

13. 梯形ABCD中，AD∥BC，过D作DE∥AB交BC于E，梯形周长为42cm，AD=6cm，则△CDE的周长是　　cm。

14. 如图已知：四边形ABCD中，AC、BD交于O，AC=BD，E、F为AB、CD中点，EF交BD、AC于MN。
　　求证：OM=ON

15. 已知是菱形的边长为5cm，一对角线长8cm，则此菱形的另一条对角线长　　　cm，它的面积为　　　cm²。

三.判断题 (本大题共 5 分)

1. 两条对角线相等的四边形是矩形。（　　）

2. 四边形的内角和等于外角和。（　 ）

3. 一个直角既是中心对称图形，也是轴对称图形。（　　）

4. 两条对角线互相垂直的四边形是菱形。（　　）

5. 两条对角线互相垂直的矩形是正方形。（　 ）

四.作图题 (本大题共 5 分)

1. 已知线段a、b，求作矩形ABCD，使AB=a， BC=b。

五.证明题 (本大题共 40 分)

1. 等腰梯形一底角为60°，一条长为2 √3cm的对角线平分这个角。求此梯形的周长。

2. Rt△ABC中，∠C=90°。CD是AB边上的中线，过A作CD的平行线，过C作AB的平行线，两线交于E。
求证：四边形ADCE是菱形

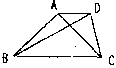
3. 如图已知：梯形ABCD中，AB∥CD，E为AD中点，且BC=AB+CD。
求证：BE⊥CE。

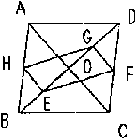
4. □ABCD中，对角线AC、BD交于O，E、F、G、H分别是BO、DC、DO、AB的中点。
求证：四边形DFGH是平行四边形

初二几何---四边形 —— 答案

一.选择题 (本大题共 20 分)

1. ：B

2. ：D

3. ：C

4. ：C

5. ：B

6. ：D

7. ：D

8. ：C

9. ：C

10. ：D

二.填空题 (本大题共 30 分)

1. ：√3，2；　　

2. ：2

3. ：互相平分且相等，互相垂直平分

4. ：30

5. ：10，2

6. ：大于8但小于32

7. ：60，120，84√3

8. ：平行四边形，14

9. ：2

10. ：证明：取AD中点G，连结EG、FG，则：EG∥BD，
　　　　　　  且EG=1/2BD，FG∥AC，
　　　　　　  且：FG=1/2AC
　　　　　　  ∵AC=BD
　　　　　　  ∴EG=FG，∠GEF=∠GFE
　　　　　　  又∵EG∥BD
　　　　　　  ∴∠GEF=∠OMN
　　　　　　  FG∥AC，∠GFE=∠ONM
　　　　　　  ∴∠OMN=∠ONM，∴OM=ON

11. ：互相平分且相等，互相垂直平分

12. ：4√3

13. ：30

14. ：解：过A作AE⊥BC于E，过D作DF⊥BC于F，则：AE=DF，
　　　　　　∵AB⊥AC， AB=AC
　　　　　　∴△ABC是等腰直角三角形
　　　　　　∴AE=BE= BC
　　　　　　又∵BD=BC， ∴AE=1/2BD
　　　　　　即：DF= BD，∴∠DBC=30°

15. ：6，24

三.判断题 (本大题共 5 分)

1. ：×

2. ：√

3. ：×

4. ：×

5. ：√

四.作图题 (本大题共 5 分)

1. ：作法：（1）作∠MBN=90°
　　　　　　  （2）在MB上截取AB=a，在NB上截取 BC=b
　　　　　　  （3）过A作EA⊥MB于A，过C作FC⊥BN于C， EA、FC交于D。四边形ABCD即为所求作的矩形。

五.证明题 (本大题共 40 分)

1. ：解：∵∠ABC=60°，BD平分∠ABC，
　　　　　　∴∠DBC=∠ABD=30°，
　　　　　　又∵∠C=∠ABC=60°
　　　　　　∴∠BDC=90°
　　　　　　在Rt△BDC中，BD=2 √3
　　　　　　∴CD= BC=2，BC=4
　　　　　　AB=CD=2
　　　　　　而AD∥BC，∠ADB=∠DBC=30°
　　　　　　∴AD=AB=2
　　　　　　∴AB+BC+CD+DA=2+4+2+2=10，答：此梯形的周长为10cm。

2. ：证明：∵AECD，CEAD，
　　　　　　  ∴四边形ADCE是平行四边形，在Rt△ABC中，CD是斜边AB上的中线。
　　　　　　  ∴CD=1/2AB=AD
　　　　　　  ∴四边形ADCE是菱形　　　

3. ：证明：延长CE交BA的延长线于F,
　　　　　　  ∵AB∥CD
　　　　　　  ∠F=∠DCE
　　　　　　　  ∴在△AFE和△DCE中
　　　　　　　  ∠F=∠DCE
　　　　　　　　  ∠AEF=∠DEC
　　　　　　　　  AE=DE
　　　　　　　 ∴△AFE≌△DCE(AAS)
　　　　　　　 ∴FA=CD　　FE=CE
　　　　　　　 E为FC中点
　　　　　　　　　　  又∵BC=AB+CD,BF=AB+AF
　　　　　　　　　　　　　　  ∴BC=BF,即：FBC是等腰三角形。
　　　　　　　　　　  ∵E为FC中点，∴BE⊥FC
　　　　　　　　　　　　　　 即：BE⊥CE

4. ：证明：□ABCD中，AB=CD， BO=DO
　　　　　　  ∵H、F分别为AB、CD中点
　　　　　　  ∴BH= AB= DC=DF
　　　　　　  又∵E、G分别为BO、DO中点，  ∴EO=1/2BO=1/2DO=GO
　　　　　　  ∴BG=BO+GO=DO+EO=DE
　　　　　　  而AB∥CD　　∴ ∠HBE=∠FDG
　　　　　　  在△BFH和△DEF中，
　　　　　　　　 BH=DF（已证）　　 ∴△BGH≌△DEF
　　　　　　　　  ∠HBE=∠FDG（已证）　　 （SAS）
　　　　　　　　  BG=DE（已证）
　　　　　　　 ∴HG=EF， ∠HGB=∠FED
　　　　　　　 ∴HG∥EF
　　　　　　　 ∴四边形EFGH是平行四边形