九、格点与面积(A)
年级 ______班 _____ 姓名 _____得分 _____
一、填空题:
 |
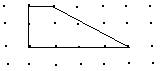1.下图的图形的面积是________(面积单位).
 |
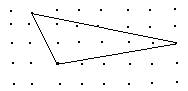2. 下列的图形中,三角形的面积是_________(面积单位).
 |
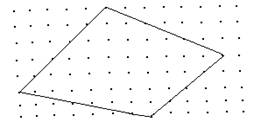3.下列多边形的面积是________(面积单位).
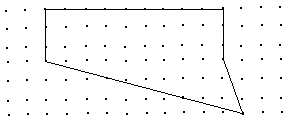
4.下列多边形的面积是_________(面积单位).
 |
5.求下列多边形的面积,填在相应的括号里:
=（ ）
=（ ）.
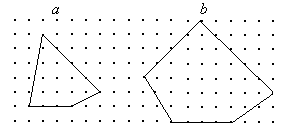
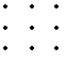6.用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?
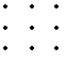
7.在右图中,如果钉与钉之间距离为1厘米,用橡皮筋将适当的三个钉子连结起来就得到一个三角形.在这些三角形中,面积等于2平方厘米的三角形有多少个？
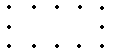
8.右图有12个点,相邻两个点之间的距离是1厘米,这些点可以连成多少个面积为2平方厘米的三角形?
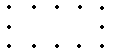9.12个钉钉成右图那样的一个矩形钉阵,相邻两钉间的距离都是1厘米.以这些钉为顶点用皮筋去套,可以得到不少三角形.问这些三角形中面积为3平方厘米的三角形有多少个?
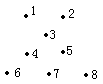
10.右图是由8个钉组成的不规则钉阵,我们依次给它们编号,分别为1,2,3,4,5,6,7,8.这1,3,5;2,3,4;6,7,8分别在一条直线上,用皮筋去套这些钉,一共可以套出多少个三角形?
二、解答题:
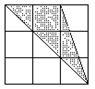
1.右图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?
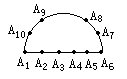
2.右图中有A1 A2 ,…,A10共10个点,以这些点为顶点,可以画多少个不同的三角形?
3.在圆周上任意给定6个点,在圆内再选4个点,使得以这10个点为顶点构成尽可能多的彼此不重叠的三角形.这些三角形最多有多少个?
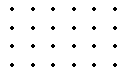4.右图是一个相邻横竖两排距离都相等的4
6矩形钉阵,你能套出多少个不同的正方形来?
———————————————答 案——————————————————————
一、填空题:
1. 5.
2. 8. 点金术:设图形内的点为V,图形边上的点为L,则面积为L
2-1+V.
3. 142-1+35=41.
4. 36. 点金术:可以分成一个长方形和三角形.
5. =10+92-1 =30+152-1
=13.5 =36.5
6. 共有32个.
解:分类统计如下:
 |  |  | |||
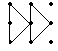
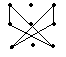
① ② ③
底为2,高为1 底为2,高为1 底为1,高为2
 |  |  | |||
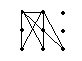3
2=6(个)
32=6(个) 32=6(个)
④ ⑤ ⑥
底为1,高为2 底为2,高为1 底为1,高为2
32=6(个) 22=4(个) 22=4(个)
所以,面积等于1平方厘米的三角形的个数有:
6+6+6+6+4+4=32(个).
7. 答:面积等于2平方厘米的三角形有8个.
8. 共有54个.
解:分类如下:
 |  |  | |||
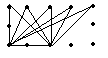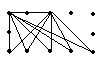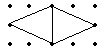① ② ③
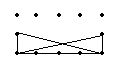
底为2,高为2 底为2,高为2 底为2,高为2
53=15(个)
53=15(个) 2(个)
 |  |  | |||
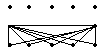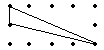④ ⑤ ⑥
底为4,高为1 底为4,高为1 底为1,高为4
52=10(个) 22=4(个) 4(个)
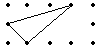
它的面积为
⑦ 42-132-112-(1+3)22
4个 =2(平方厘米)
所以,面积为2平方厘米的三角形有:
15+15+2+10+4+4+4=54(个).
9. 答:面积为3平方厘米的三角形有26个.
10. 解:由于“不在一条直线上的三点可确定一个三角形”,根据排列组合知识得,一共可套出三角形:
876(321)-1-1-1=56-3=53(个).
这里减去的3个三角形,实际上是不能构成的.因为1,3,5;2,3,4;6,7,8分别在一条直线上.
二、解答题:
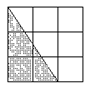
1. 解: ① 设每个小正方形的边长为1个长度单位,则阴影三角形面积为:
232=3(面积单位).
 |  |  | |||
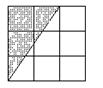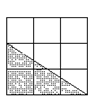②分类统计如下:
① ② ③
底为2,高为3 底为2,高为3 底为3,高为2
42=8(个) 42=8(个)
42=8(个)
 |  |  | |||
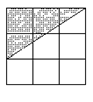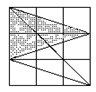④ ⑤ ⑥
底为3,高为2 底为2,高为3 底为3,高为2
42=8(个) 222=8(个) 222=8(个)
③与阴影三角形面积相同的三角形有:
8+8+8+8+8+8=48(个).
2. 答:可画100个.
提示:将所有的三角形按有一个顶点在直径上和两个顶点在直径上及三个顶点都不在直径上的三类.
3. 答:12 个.
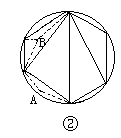
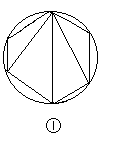
提示:对任意给定的6 个点可以构成4个互不重叠的三角形(图①),下图②中如果选取A点只能增加一个互不重叠的三角形,如果选取B点可以增加两个互不重叠的三角形,所以只要在图①的4个三角形内各取一点,就得到12个互不重叠的三角形.
4.一共能套出40个正方形.