初中数学二年级(下)第十章新概念梯级测试卷
●测试内容：数的开方
●测试时间：90分钟 ●测试总分：120分(培优20分)
基础知识达纲检测
一、选择题(2′×15)
1.下列语句正确的是( )
A.无理数都是无限小数 B.无限小数都是无理数
C.有理数都是有限小数 D.带根号的数都是无理数
2.(-6)2的平方根是( )
A.-6 B.6 C.±6 D.不存在
3.一个正数N扩大到原来的100倍，则它的算术平方根扩大到原来的( )
A.10倍 B.100倍 C.1000倍 D.以上都不对
4.下列各结论中，正确的是( )
A.-
＝-5
B.(-
)2＝9
C.
＝±16
D.-(-
)2＝
5.与数轴上的点有一一对应关系的数是( )
A.自然数 B.有理数 C.无理数 D.实数
6.在π，0，0.……，
，3.，｜１｜，，0.
这8个数中无理数的个数是( )
A.1 B.2 C.3 D.4
7.负数的奇次方根是( )
A.一个正数 B.一个负数 C.两个互为相反数 D.不存在
8.在下列条件中不能保证
是实数的是( )
A.n为正整数，a为实数 B.n为正整数，a为非负数
C.n为奇数，a为实数 D.n为偶数，a为非负数
9.当a是负数，n是奇数时，a的n次方根记作( )
A.
B.- C. D.±
10.
-
＝2，则n是( )
A.3 B.偶数 C.奇数 D.任意实数
11.设m＝-
，n＝-3
，那么m与n的大小关系是( )
A.m＞n B.m＜n C.m＝n D.m≤n
12.下列说法中，正确的是( )
A.27的立方根是3，记作＝3
B.-25的算术平方根是5
C.a的三次立方根是±
D.正数a的算术平方根是
13.已知a和｜a｜互为相反数，则a( )
A.为任意实数 B.为非正实数 C.为非负实数 D.等于0
14.下列各式中，不正确的是( )
A.
＞
B.
＜
C.
＞
D.＝｜-5｜
15.若a为实数，则下列叙述正确的是( )
A.｜-a｜是正数 B.-｜a｜是负数
C.
是非负数
D.｜-a｜永远大于-｜a｜
二、填空题(3′×10)
1.的算术平方根是___________，平方根是___________.
2.
的平方根是___________，算 术平方根是___________.
3.a2的平方根是___________，若a＜0，则a2的算术平方根是___________
4.若
＝8.400，则
＝___________ ，
≈___________＝___________.
5.一个直角三角形的两直角边的长分别是
和4，则斜边长是
.
6.一个数的立方是它本身，这个数是___________.
7.
的立方根是___________，若(x-1)3＝1，则x＝ ___________.
8.能使
有意义的a值是___________.
9.已知x、y是实数，且｜x+
｜+
＝0，则xy＝
10.如果的平方根是±3，那么a＝___________.
三、计算题 (4′×5)
1.
2.0.1
+0.2
3.
-
+
4.+
+
(精确到0.01)
5.｜1-｜+｜-｜+｜- 2｜
四、解方程(4′×4)
1.x2-8＝0 2.8x3＝27
3.(x+2)2-25＝0
4.(
-10)3＝27000
五、解答题
1.在实数范围内分解因式x4-9.(4′)
2.若a的倒数是-
，
的相反数是0 ，c是-1的立方根，求 
+
+
的值.(5′)
3.若
与｜x+y-3｜互为相反数，求-5x2-y的值.(5′)
4.已知k是2的算术平方根，求x-k＜7的正整数解.(5′)
5.已知一个正方形的棱长是5cm，再做一个正方体，使它的体积是原正方体体积的2倍，求所 做的正方体的棱长(已知
＝1.260，精确到0.1)(5′)
初中数学二年级(下)第十章新概念梯级测试卷
●测试内容：数的开方
●测试时间：90分钟 ●测试总分：120分(培优20分)
重点难点过关测试
一、选择题(2′×15)
1.下列命题中正确的是( )
A.带根号的数都是无理数 B.不带根号的数一定是有理数
C.无限小数都是无理数 D.无理数一定是无限不循环小数
2.在数0.3，
，3.14，
，-2.13中无理数有( )
A.1个 B.2个 C.3个 D.5个
3.已知
＝4.098，
＝40.98，则x等于( )
A.688 B.6880 C.68800 D.688000
4.
的平方根是( )
A.3 B. C.±3 D.±
5.全体小数所在的集合是( )
A.分数集合 B.有理数集合 C.无理数集合 D.实数集合
6.如果
＝4，那么(a-2)2的值等于( )
A.4 B.12 C.100 D.196
7.下列语句中，正确的是( )
A.无理数是开方开不尽的数
B.8的立方根是±2
C.绝对值等于
的实数是
D.每一个实数都有数轴上的一个点与它对应
8.已知a是小于
+的整数，且｜2-a｜＝a-2，则满足条
件的a的个数是( )
A.6 B.5 C.4 D.13
9.已知a＝-3+，b=-3.5+
，c＝-3
+
，则a、b、c的大小关系是( )
A.a＞b＞c B.b＞c＞a C.a＞c＞b D.c＞b＞a
10.下列各式中：
＝
，
＝0.1，-
＝-32，-
＝-27，计算 正确的有( )
A.1个 B.2个 C.3个 D.4个
11.设a、b均为负实数，且｜a｜＞｜-b｜，则( )
A.a＞-b B.a＜b C.-a＜-b D.a＞b
12.下列语句中正确的是( )
①无理数与-的和是有理数 ②无理数
与的和是无理数 ③两个无理数的和不一定是无理数
A.①② B.①③ C.②③ D.①②③
13.若x为实数，则实数y＝｜｜
-1｜-2｜的值( )
A.无法确定 B.只能等于3 C.只能等于1 D.非上述答案
14.若3m＜-1，则
+
化简为( )
A.-5m B.-m-2 C.m D.5m
15.等式＝()2成立的条件是( )
A.a是任意实数 B.a＞0 C.a＜0 D.a≥0
二、填空题(3′×10)
1.等式
＝x成立的条件是
，等式
＝-y成立的条件是___________，等式
＝｜m｜成立的条件是
.
2.若
＝x，且
＝
，则y＝
.
3.已知x2＝64，则＝___________.
4.已知
+｜2x-y-5｜＝0，则x＝
，y＝
.
5.已知
＝4.858，
＝1.536，则-
＝___________.
6.某数与它的倒数和的平方等于4，这个数是___________.
7.设m＜0，化简｜m｜+-
＝
.
8.若(x-1)２+｜y+2｜+
＝0，那么(x+1)2+(y-2)2+(z-3)2的平方根
为___________，y＝___________.
9.若与｜x+y-3｜互为相反数，则x＝___________，y＝ ___________.
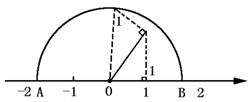
10.观察右边的图形，点A、B所表示的实数分别是___________.
三、计算题(4′×4)
1.
-
2.
+
3.
×(-
)
4.
四、解答题 (6′×3)
1.已知144x2＝49，且y3+8＝0，求x+y的值.
2.y＝
+
+x3，求
的值.
3.已知A＝
是m+n+3的算术平方根，B＝
是m+2n的立方根.求B-A的立方根.
五、应用问题(6′)
有一边长为11cm的正方形和一个长为15cm，宽为5cm的矩形，要作一个面积为这两个图形面积之和的正方形，问边长应为多少厘米?
思维发散培优测试 (20分)
1.若a、b为有理数，且a+b＝(1-)2，求ab的值。(8 ′)
2.比较下面两列计算式结果的大小(在横线上选填“＞”、“＜”、“＝”)(12′)
42+32 2×4×3 (-2)2+12 2×(-2)×1
()2+(
)２ 2×× 22+22 2×2×2
……
通过观察归纳，写出能反映这种规律的一般结论，并加以证明。
初中数学二年级(下)第十一章新概念梯级测试卷
●测试内容：二次根式
●测试时间：90分钟 ●测试总分：120分
基础知识达纲检测
一、选择题(2′×15)
1.把根式-a
化为最简二次根式是( )
A. B.
C.- D.-
2.如果根式
与
是同次根式 ，则m的值是( )
A.15
B.1 C. D.5
3.计算：2
-3
-
+
的结果是( )
A.
B.
C.
D.
4.若x＞0，y＞0，则化简x
÷y
×
等于( )
A.
B.
C. D.xy
5.若x＞y，则根式(y-x)
化简的结果是( )
A.
B.-
C.-
D.
6.如果
是二次根式，那么( )
A.a≤0 B.a≥0 C.a＜0 D.a＞0
7.若x＝-1，则
的值是( )
A. B.±
C.2 D.±2
8.下列二次根式中，为最简二次根式的是( )
A.
B.
C.
D.
9.下列说法中，正确的是( )
A.同类二次根式必都是最简二次根式
B.最简二次根式必都是同类二次根式
C.同类二次根式不一定都是最简二次根式
D.任何两个二次根式都可以化为同类二次根式
10.化简：
(0＜x＜y＝得( )
A.±(x+y)(x-y) B.y2-x2
C.x2-y2 D.以上答案都不对
11.计算：
得 ( )
A.--
B.- C.--2 D. +
12.当a为整数，且-3＜a＜-1时，式子
-的值为( )
A.-3 B.3 C.1 D.-1
13.等式
＝
·
成立，那么实 数k的值是( )
A.k≥1或k≤-1 B.k≥-1
C.k＞1 D.k≥1
14.已知1＜x＜2，则
+
的值是( )
A.-2 B.2 C.0 D.以上答案都不对
15.若
+｜2x+y-7｜＝0，则x，y的值是( )
A.
B.
C.
D.
二、填空题 (3′×10)
1. -1的相反数的倒数是___________.
2.
与
是同类根式，则a＝
，b＝___________.
3.化简：当0＜x＜1时，
+x2＝___________ .
4.计算：(3
-2
)+(2
-
)＝___________.
5.当x≥0，y≥0时，
-
＝___________.
6.已知x＞0，y＞0，计算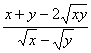
＝___________.
7.当a＞1时，化简a-
＝___________.
8.已知x＝+1，则(x+
)2-4(x+)+4的值是___________.
9.若
＝
·
成立，则x应满足的 条件是___________.
10.若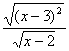
有意义，则x的取值范围是___________.
三、计算题 (5′×5)
1.2
-3
+4
-7
2.
+1÷(-2)-(2+)+｜2-｜+()-2
3.÷(5-)-(-)2
4.
+
-
-
5.(
-
)÷
四、化简求值
1.已知x＝+1，y＝-1，求
的值.(5′)
2.已知x＝+，求x2-2x+5的值.(6′)
3.当x＝
，y＝
时，求
的值.(6′)
4.已知x2+y2-2y+1＝0，求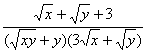
的值.(6′)
五、解方程(6′×2)
1. (x+1)＝ (x-1)
2.
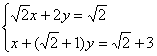
初中二年级数学(下)第十一章新概念梯级测试卷
●测试内容：二次根式
●测试时间：90分钟 ●测试总分：100分(培优20分)
重点难点过关测试
一、选择题(3′×8)
1.在根式
、
、
、
、
中，最简二次根式有( )
A.1个 B.2个 C.3个 D.4个
2.在二次根式
，-
，
，
和
中，与是同类根式的有 ( )
A.2个 B.3个 C.4个 D.5个
3.在下列各式中，等号不成立的是( )
A.
＝-
B.2x＝
(x＞0)
C.
＝a
D.(x+2+y)÷(
+)＝+
4.在下列各式的化简中，化简正确的有( )
①
＝a ②5x-＝4 x ③6a
＝
④
+
＝10
A.1个 B.2个 C.3个 D.4个
5.已知二条线段的长分别为cm、cm，那么能与它们组成 直角三角形的第三条线段的长是( )
A.1cm B.cm
C.5cm
D.1cm或cm
6.已知a＜0，化简：
的结果是 ( )
A.1 B.-1 C.0 D.2a
7.若
＝
，则k是( )
A.1 B.
C.3 D.
8.设的小数部分为b，那么(4+b)b的值是( )
A.1 B.是一个有理数 C.3 D.无法确定
9.当x＜2y时，化简：
得( )
A.x(x-2y)
B.
C.(x-2y)
D.(2y-x)
10.若x＜1且y＝
+3，则y
÷
×
的值是( )
A.
B.4 C.16 D.64
11.当x＜0时，化简：｜x｜+
的结果是( )
A.-1 B.1 C.1-2x D.2x-1
12.化简：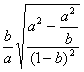
(a＞0，b＞1)的结果是( )
A.
B.
C.
D.
13.化简：｜2a+3｜+
(a＜-4＝的结 果是( )
A.
-3a
B.3a- C.a+ D. -3a
14.当a＞0，b＞0时，n是正整数，计算：
的结果是( )
A.(b-a)
B(anb3-an+1b2)
C.(b3-ab2)
D.(anb3+an+1b2)
15.
·
的积为 ( )
A.1
B.17 C.
D.
二、填空题(3′×10)
1.2+a-的有理化因式是
.
2.当m＞n时，化简：(m-n)·
＝
.
3.已知-2＜m＜-1，化简：
-
＝___________.
4.当a＜-b＜1时，化简：
÷
的结果为___________.
5.
·
＝___________.
6.计算：(a+2+b)÷(+)-(-)＝___________.
7.化简：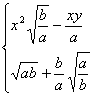
÷x2y2
(a＞0，b＞0)＝___________.
8.若菱形两对角线长分别为(2+3)和(2-3)，则菱形面积＝___________.
9.已知b＜0，化简：-
-+
＝
.
10.
＝___________.
三、计算题(4′×3)
1.÷(
+
)+
2.［(
)2+
］·
3.( +2-)(-2 +)
四、化简下列各式(5′×2)
1.(x-y)
+
2.
·(
-
)÷
÷(a+b-2)
五、解答题(6′×3)
1.已知x、y为实数，且y＝
+
+，求5x+｜2y-1｜-
的值 .
2.已知x、y为正数，且(+)＝3(+5)，求
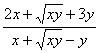的值.
3.设x、y是实数，且x2+y2-2x+4y+5＝0，求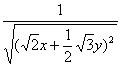
.
思维发散培优测试 (20分)
1.m是的小数部分，求
的值.(8′)
2.观察下列各式及其验证过程：
2＝
.
验证 ：2＝
＝
＝
＝
3
＝
.
验证：3＝
＝
＝
＝ (12′)
按照上述两个等式及其验证过程的基本思路，猜想4
的变形结果并进行验证.
初中数学二年级(下)第四章新概念梯级测试卷
●测试内容：四边形
●测试时间：90分钟 ●测试总分：120分(培优20分)
基础知识达纲检测
一、选择题 (2′×15)
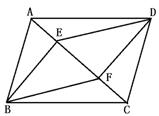
1.如右图，点E、F是ABCD对角线AC上两点，且AE＝CF.图中全等三角形共有( )
A.3对 B.4对
C.6对 D.12对
2.如果一个多边形的每一个外角都是锐角，那么这个多边形的边数一定不小于( )
A.3 B.4 C.5 D.6
3.下面命题正确的是( )
A.两条对角线相等的四边形是矩形
B.一组对边平行，另一组对边相等的四边形是平行四边形
C.对角线互相平分且相等的四边形是正方形
D.对角线互相垂直的平行四边形是菱形
4.如右图，已知△ABC与△CDA关于点O对称，过O任作直线EF交AD、BC分别于点E、F，下面的 结论：①点E和F、B和D是关于中心O的对称点；②直线BD必经过点O；③四边形ABCD是平行四 边形；④四边形DEOC与四边形BFOA必全等，其中正确的结论的个数有( )
A.1个 B.2个 C.3个 D.4个
5.下面说法正确的是( )
A.全等的两个图形成中心对称
B.成中心对称的两个图形必须重合
C.成中心对称的两个图形全等
D.旋转后能重合的两个图形中心对称
6.在平行四边形，矩形、菱形、正方形、等腰梯形中，对角线相等的图形有( )
A.2个 B.3个 C.4个 D.5个
7.四边形ABCD中，∠A∶∠B∶∠C∶∠D＝3∶3∶2∶4，则此四边形是( )
A.一般四边形 B.平行四边形 C.直角梯形 D.等腰梯形
8.在线段、角、等边三角形、平行四边形、矩形、菱形、等腰梯形等图形中，既是轴对称图 形，又是中心对称图形的个数是( )
A.6个 B.5个 C.4个 D.3个
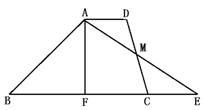
9.如右图，梯形ABCD中，AD∥BC，AF⊥BC，M是CD的中点，∠B＝45° ，AF＝4，EF＝7，则梯形ABCD的面积是( )
A.22 B.24
C.26 D.28
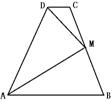10.如右图，M为梯形ABCD腰BC的中点，AM、DM分别平分∠DAB、∠ADC，AB＝a，DC＝b，则AB 等于( )
A.a-b
B. (b+a)
C.a+b D.不能确定
11.若等腰梯形两底的差等于一腰长，那么它的腰与下底的夹角为( )
A.30° B.45° C.60° D.75°
12.以3、5、5、11为边作梯形，这样的梯形( )
A.有一个 B.有两个 C.有三个 D.不存在
13.过多边形的一个顶点引对角线，把多边形分成10个三角形，则多边形边数为( )
A.12 B.11 C.10 D.9
14.已知菱形的一条边长是两条对角线长的比例中项，那么菱形的一个锐角是( )
A.30° B.45° C.60° D.90°
15.平行四边形的四个内角平分线围成的四边形是( )
A.菱形 B.矩形 C.正方形 D.平行四边形
二、填空题(3′×10)
1.一个多边形的内角和是外角和的9倍，这个多边形的边数是___________.
2.一多边形的每一个内角都相等，它的内角和与外角和的总和为1620°，这个多边形的每一 个外角等于___________.
3.一平行四边形两条对角线的长度分别是5cm和7cm，一边长为acm，则a的取值范围是___________.
4.如右图，AE、AF是ABCD的两条高，∠EAF＝135°，BC＝６cm，AB＝8cm，则∠C＝ 度；AF＝ cm；AE＝ cm；A BCD的面积为___________.
5.若矩形两条对角线所夹锐角为60°，且对角线长12cm，则矩形两边为 .
6.P是正方形ABCD内一点，△PAB为等边三角形，若正方形的面积为1，则△PBC的面积等于
___________.
7.等腰梯形的上底与它的高相等，下底是上底的3倍，则梯形最大的内角等于 度.
8.梯形ABCD中，AD∥BC，∠B与∠C互余，若∠C＝30°，AD＝2cm，BC＝8cm，则AB的长是 .
9.梯形ABCD中，AD∥BC，P是DC的中点，若梯形的面积为6cm2，则△ABP的面积为 .
10.梯形的中位线长16cm，被一条对角线分成两段，这两段之差为6cm，则梯形上底长等于 .
三、解答题
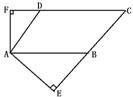
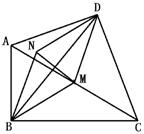
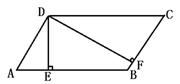
1.如下图，已知△ABE、△BCF、△FED都是等边三角形，求证：四边形ABCD是平行四边形.(8 ′)
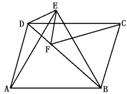
2.已知：AD是Rt△ABC斜边上的高，BE平分∠B交AD于G、AC于E，过E作EF⊥BC于F.求证：四边形AEFG为菱形.(8′)
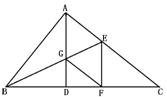
3.梯形ABCD中，AB∥CD，以AD、AC为邻边作平行四边行ACED，DC延长线交BE于F，求证：F是BE的中点 .(8′)
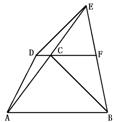
4.平行四边形ABCD中，以AC为斜边作Rt△ACE，又∠BED为直角，求证：四边形ABCD是矩形. (8′)
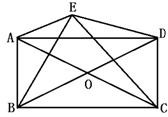
5.如下图，从矩形ABCD的顶点C作对角线BD的垂线与∠BAD的平分线相交于点E，求证：CE ＝BD.(8′)
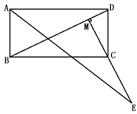
6.如下图，正方形ABCD的对角线交于O点，E为OA上任意一点，CF⊥BE于F，CF交OB于G，求证 ：OE＝OG.
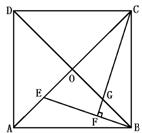
7.如下图，四边形ABCD中，∠ABC＝∠ADC＝90°，M是AC的中点，MN⊥BD与MD的平行线BN相 交于N.
①试问四边形BNDM是何四边形?证明你的结论.
②若∠DCA＝30°，∠BAC＝45°，求四边形BNDM各内角的度数.
初中二年级数学(下)第四章新概念梯级测试卷
●测试内容：数的开方
●测试时间：90分钟 ●测试总分：120分(培优20分)
重点难点过关测试
一、选择题(3′×15)
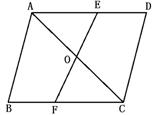
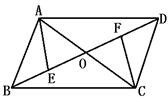1.如右图，在平行四边形ABCD中，对角线AC、BD交于O，点E、F在BD上，且BE＝EO，OF＝FD，则图中关于点O成中心对称的三角形有( )
A.4对 B.5对
C.6对 D.7对
2.如果把一个多边形的边数增加，则所有外角的平均值( )
A.增大 B.减小
C.不变 D.无法确定
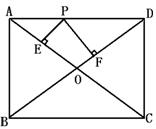
3.矩形ABCD的长BC＝4，宽AB＝3，P是AD上任一点，过点P作PE⊥AC 、PF⊥BD，垂足分别为E、F，则PE+PF的长为( )
A.2 B.2.4
C.2.5 D.3
4.矩形各内角的平分线组成的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
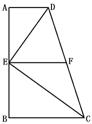5.如右图，直角梯形ABCD中，AD∥BC，∠B＝90°，EF是中位线，ED、EC分别平分∠ADC和∠ BCD.下面的结论：①△DEC是直角三角形；②AD+BC＝DC；③点E到DC的距离等于AB；④DE·EC＝EF·AB，其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
6.如右图，平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，若平行四边形ABCD的周长为48 ，DE＝5，DF＝10，则平行四边形ABCD的面积等于( )
A.87.5 B.80
C.75 D.72.5
7.梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，若∠B与∠C互余，则2MN与BC-AD的关系 是( )
A.2MN＜BC-AD B.2MN＝BC-AD
C.2MN＞BC-AD D.无法确定
8.梯形的上底为a，下底为b，则梯形被其中位线分成的两部分面积之比为( )
A.
B.
C.
D.
9.一梯形的中位线将梯形的面积分成1∶2，则上底a，中位线b，下底c之比为 ( )
A.1∶2∶3 B.1∶2∶5 C.3∶4∶5 D.1∶3∶5
10.已知矩形的周长为p，对角线长为d，那么矩形的长与宽之差为( )
A.
B.
C.
D.
11.等腰梯形两底为4cm，10cm，面积为21cm2，则较小的底角是( )
A.30° B.45° C.60° D.90°
12.正方形ABCD的边长为1，E是AC上一点，且AE＝1，EF⊥AC交BC于F，则下列结论成立的是 ( )
A.BF＝
B.BＦ＝-1 C.BF＝ D.BF＝
(2-1)
13.等腰梯形的两条对角线互相垂直，那么梯形的高h和中位线长m的大小关系是( )
A.m＞h B.m＜h C.m＝h D.不能确定
14.在梯形ABCD中，已知AB∥CD，E是BC的中点，设△EDA的面积为S1，梯形的面积为S2 ，则S1与S2的关系是( )
A.S1＝S2 B.S1＝
S2 C.S1＝
S2 D.S1＝
S2
15.在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E、F分别为BC、CD的中点，则∠EAF等于( )
A.75° B.60° C.45° D.30°
二、填空题(3′×10)
1.每个内角都相等的多边形，它的一个外角等于一个内角的，这个多 边形的边数是___________.
2.若多边形的内角和与外角和之比为9∶2，则这个多边形的边数是 .
3.以正方形ABCD的边AB向外作等边三形ABE，BD交CE于F，则∠AFD的度数为＝ .
4.平行四边形ABCD的周长为48cm，对角线相交于O，△AOB的周长比△BOC的周长多4cm，则AB、BC的长 分别等于___________.
5.矩形ABCD中，M是BC的中点，MA⊥MD.如果矩形的周长为48cm，则矩形的面积等于 .
6.在△ABC中，BD、CE分别是边AC、BA上的中线，M、N分别是BD、CE的中点，若BC＝4.8cm， 则MN的长为___________.
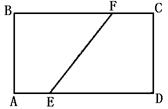
7.如下左图，在矩形ABCD中，AB＝6cm，BC＝８cm，若将矩形折叠，使B点与D点重合，则折 痕EF的长为___________.
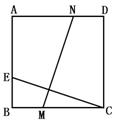
8.如上右图，四边形ABCD是正方形，CE＝MN，∠MCE＝35°，那么∠ANM 等于 .
9.若等腰梯形两底的差等于一腰长，那么它的腰与下底的夹角为 .
10.等腰梯形ABCD中，AB∥DC，AH⊥DC，垂足为H，若DC＝2AB，AH＝8，中位线长6，则腰AD 的长等于___________.