初中几何第五章《相似形》测试题
一、填空题（每小题2分，共32分）
⒈一个矩形的长为10cm，宽为40mm，长与宽的比为 ；
⒉已知线段b＝5cm，c＝10cm，d＝7cm，那么b、c、d的第四比例项a＝ ；
⒊已知：
，那么ad＝ ，
＝ ；
⒋已知
，且2a＋3b－c＝26，则a－b＋c＝
;
⒌如果(x＋3):x＝12:7,那么x＝
；
⒍如果
，则
＝
；
⒎若ａ＝６，ｂ＝８，则ａ与ｂ的比例中项ｘ＝ ；
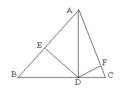
⒏如图，AD⊥BC，DE⊥AB，DF⊥AC，则AE·AB＝AC· ；
⒐已知一个三角形三边上高的比为ha:hb:hc＝2:3:4，则三边的比为a:b:c＝ ；
⒑在Rt△ABC中‚∠C＝90°,CD⊥AB于D，AC＝2，BD＝2则AD＝ ，BC＝ ；
⒒梯形两底的比AD:BC＝1:2，对角线AC与BD交于O，若S△AOD＝２cm2,则S△ABC＝ ；
⒓已知一个三角形三边的比是4:5:6，顺次连结三边中点所得三角形的周长为30cm，则原三角形的最长边长为 ；
⒔已知D为△ABC的BC边上的中点，AB＝2AD，∠ADB和∠ABC的平分线分别交AB、AC于M、
N，那么MN与BC的关系是 ；
⒕已知矩形的周长为20cm，两邻边的差为4cm，那么矩形两邻边的比等于 ；
⒖在Rt△ABC中‚∠C＝90°，CD为角平分线，且AD:DB＝4:5，则AB:BC:AC＝ 。
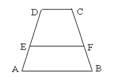⒗如图，梯形ABCD中，DC∥AB，DC＝3，AB＝5，AD＝8，E是DA的黄金
分割点，且EF∥AB交BC于点F，则EF＝ 。
二、选择题（每小题3分，共18分）
⒈在△ABC中‚D、F在AB上，E、G在AC上，且DE∥FG∥BC，若DE:FG:BC＝1:2:3，则
AD:DF:FB的比值为【 】
A、1:2:3 ； B、1:1:1 ； C、1:2:6 ； D、1:4:9 。
⒉下列各组条件，不能判定△ABC与△A/B/C/相似的是【 】
A、∠A＝∠A/，∠B＝∠B/； B、∠C＝∠C/＝90°，∠A＝12°，∠B/＝78°；
C、∠A＝∠B，∠B/＝∠A/； D、∠A＋∠B＝∠A/＋∠B/，∠A－∠B＝∠A/－∠B/。
⒊下列说法不正确的是【 】
A、相似三角形的对应边的比叫做相似比； B、全等三角形一定相似；
C、相似三角形一定全等； D、若△ABC∽△A1B1C1，△A1B1C1∽△A2B2C2 ，则△ABC∽△A2B2C2
⒋在相同时刻，物高与影长成比例，现测得一建筑物的影长为50米，高1.5米测杆的影长为2.5米，那么建筑物的高度为【 】
A、30米； B、40米； C、35米； D、以上都不对。
⒌如图，梯形ABCD中，AD∥BC，AC、BD相交于P，若S△BPC:S△ABC＝2:3，
则S△BPC:S△ABD等于【 】
A、4:3 ； B、8:5 ； C、1:1 ； D、3:2 。
⒍在Rt△ABC中‚∠A＝90°，AD⊥BC于D，则等式：①BC2－AB2＝AC2，②AB2＝BD·BC，
③AC2＝BC·DC，④AD2＝BD·DC中正确的个数是【 】
A、4个 ； B、3 个； C、2 个； D、1个 。
三、计算题（每小题6分，共18分）
⒈已知：△ABC中‚AD⊥BC于D，BD＝3cm，DC＝4cm，AD＝ cm，求∠BAC的度数。
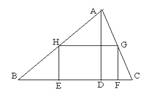⒉如图，△ABC中‚AD⊥BC于D，矩形EFGH的四个顶点在三角形三边上，已知BC＝9cm，
AD＝8cm，EF＝5cm，求矩形EFGH的面积。
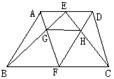
⒊如图，梯形ABCD中，AD∥BC，AD＝m，BC＝n，E、F分别是AD、BC的中点，AF与BE相交于G，CE与DF相交于H，求GH的长。
四、证明题（每小题8分，共32分）
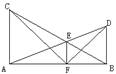
⒈如图，AC⊥AB，BD⊥AB，AD与BC相交于点E，EF⊥AB于F。
求证：∠AFC＝∠BFD。
⒉如图，已知D是△ABC中AC边的中点，过D的任意直线交AB于E，交BC的延长线于F。
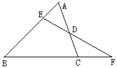求证：BE·CF＝BF·EA 。
⒊已知：AD是△ABC(AB>AC)的角平分线，AD的垂直平分线和BC的延长线交于点E。
求证：DE2＝BE·CE。
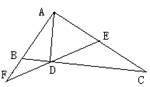⒋已知：如图，在△ABC中，∠BAC＝90°，AD⊥BC于D，E是AC的中点，ED的延长线交AB的延长线于F。求证：AB:AC＝DF:AF。