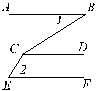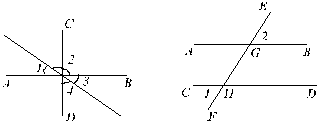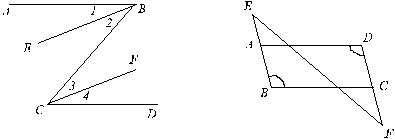初中几何第二章“相交线、平行线”能力自测题
（满分100分，时间90分）
1．判断题：（每小题3分，共24分）
（1）和为
的两个角是邻补角；
（ ）
（2）如果两个角不相等，那么这两个角不是对顶角 （ ）
（3）两条直线被第三条直线所截，同位角相等 （ ）
（4）如果直线
∥
，那么
∥
（
）
（5）两条直线平行，同旁内角相等； （ ）
（6）邻补角的角平分线所在的两条直线互相垂直 （ ）
（7）两条直线相交，所成的四个角中，一定有一个是锐角 （ ）
（8）如果直线
那么∥
（
）
2． 选择题：（每小题5分，共20分）
（1）下列语句中，正确的是（ ）
（A）有一条公共边且和为的两个角是邻角；
（B）互为邻补角的两个角不相等
（C）两边互为反向延长线的两个角是对顶角
（D）交于一点的三条直线形成3对对顶角
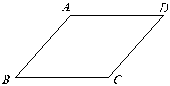
（2）如图，如果AD∥BC，则有
|
|
①∠A+∠B=
②∠B+∠C=
③∠C+∠D=
上述结论中正确的是（ ）
（A） 只有①
（B） 只有②
（C） 只有③
（D）只有①和③
|
|
（3）如图，如果AB∥CD，CD∥EF，那么∠BCE等于（ ）
（A）∠1+∠2
（B）∠2-∠1
（C）-∠2 +∠1
（D）-∠1+∠2
（4）如果直线∥，∥，那么∥。这个推量的依据是（ ）
（A）等量代换
（B）平行公理
（C）两直线平行，同位角相等
（D）平行于同一直线的两条直线平行
3． 填空：（每空1分，共16分）
|
|
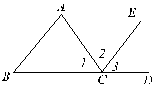
（1）如图，∠3与∠B是直线AB、______被直线______所截而成的______角；∠1与∠A是直线AB、______被直线______所截而成的______角；∠2与∠A是直线AB、______被直线______所截而成的______角。
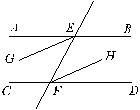
（2）已知：如图，AB∥CD，EF分别交于AB、CD于E、F，EG平分∠AEF，FH平分∠EFD。
求证： EG∥FH
|
|
证明：∵ AB∥CD（已知）
∴ ∠AEF=∠EFD （______）
∵ EG平分∠AEF，FH平分∠EFD（______），
∴∠______=
∠AEF，
∠______=∠EFD（角平分线定义）
∴ ∠______=∠______
∴ EG∥FH（______）
4． 已知：如图，∠1=
，AB⊥CD，垂足为O，EF经过点O。求∠2、∠3、∠4的度数。（10）
|
|
5． 已知：如图，直线EF与AB、CD分别相交于点G、H，∠1=∠3。
求证：AB∥CD。（10分）
6． 已知：如图，AB∥CD，BE∥CF。
求证：∠1=∠4。（10分）
7． 已知：如图，BE∥DF，∠B=∠D。求证：AD∥BC。（10分）
|
|
初中几何第二章“相交线、平行线”能力自测题
参考答案
1．（1）× （2）√ （3）× （4）× （5）× （6）√ （7）× （8）√
2．（1）C （2）D （3）C （4）D
3．（1）CE，BD，同位；BD，AC，同旁内；CE，AC，内错
（3）两直线平行，内错角相等，已知，∠GEF，∠EFH，∠GEF，∠EFH，内错角相等，两直线平行
4．∠2=
，∠3= ∠4=
5．证明：∵∠1=∠GHD，∠3=∠AGH（对顶角相等），
∠1=∠3（已知），
∴∠AGH=∠GHD
∴AB∥CD（内错角相等，内错角相等）
6．证明：∵AB∥CD（已知），
∴∠ABC=∠BCD（两条直线平行，内错角相等）
∵BE∥CF（已知）
∴∠2=∠3（两条直线平行，内错角相等），
∵∠ABC=∠1+∠2，∠BCD=∠3+∠4，
∴∠1=∠4
7． 证明：∵BE∥DF（已知）
∴∠D=∠EAD（两条直线平行，内错角相等），
∵∠B=∠D（已知），
∴∠B=∠EAD
∴AD∥BC（同位角相等，两直线平行）