十八 逻辑推理（一）
年级 班 姓名 得分
一、填空题
1. 甲、乙、丙三人进行跑步比赛.A、B、C三人对比赛结果进行预测.A说:“甲肯定是第一名.”B说:“甲不是最后一名.”C说:“甲肯定不是第一名.”其中只有一人对比赛结果的预测是对的.预测对的是 .
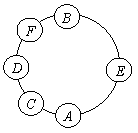
2. A、B、C、D、E和F六人一圆桌坐下.
B是坐在A右边的第二人.
C是坐在F右边的第二人.
D坐在E的正对面,还有F和E不相邻.
那么,坐在A和B之间的是 .
3. 甲、乙、丙、丁与小明五位同学进入象棋决赛.每两人都要比赛一盘,每胜一盘得2分,和一盘得1分,输一盘得0分.到现在为止,甲赛了4盘,共得了2分；乙赛了3盘,得了4分；丙赛了2盘，得了1分；丁赛了1盘，得了2分.那么小明现在已赛了 盘，得了 分.
4. 曹、钱、刘、洪四个人出差，住在同一个招待所.一天下午,他们分别要找一个单位去办事.甲单位星期一不接待,乙单位星期二不接待,丙单位星期四不接待,丁单位只在星期一、三、五接待，星期日四个单位都不接待.
曹:“两天前,我去误了一次,今天再去一次,还可以与老洪同走一条路.”
钱:“今天我一定得去,要不明天人家就不接待了.”
刘:“这星期的前几天和今天我去都能办事.”
洪:“我今天和明天去,对方都接待.”
那么,这一天是星期 ,刘要去 单位,钱要去 单位,曹要去 单位,洪要去 单位.
5. 四位外国朋友住在十八层高的饭店里,他们分别来自埃及、法国、朝鲜和墨西哥.
(1)A住的层数比C住的层数高,但比D住的层数低；
(2)B住的层数比朝鲜人住的层数低；
(3)D住的层数恰好是法国人住的层数的5倍；
(4)如果埃及人住的层数增加2层,他与朝鲜人相隔的层数,恰好和他与墨
西哥人相隔的层数一样；
(5)埃及人住的层数是法国人和朝鲜人住的层数的和.
根据上述情况,请你确定A是 人,住在 层；B是 人,住在
层；C是 人,住在 层；D是 人,住在 层.
6. 小赵的电话号码是一个五位数,它由五个不同的数字组成.小张说：“它是84261.”小王说：“它是26048.”小李说：“它是49280.”小赵说：“谁说的某一位上的数字与我的电话号码上的同一位数字相同，就算谁猜对了这个数字.现在你们每人都猜对了位置不相邻的两个数字.”这个电话号码是 .
7. 小赵的电话号码是一个五位数,它由五个不同的数字组成.小王说：“它是93715.”小张说：“它是79538.”小李说：“它是15239.”小赵说：“谁说的某一位上的数字与我的电话号码上的同一位数字相同，就算谁猜对了这个数字.现在你们三人猜对的数字个数都一样,并且电话号码上的每一个数字都有人猜对.而每个人猜对的数字的数位都不相邻”.这个电话号码是 .
8. A、B、C、D四人定期去图书馆，四人中A、B二人每隔8天(中间空7天,下同)、C每隔6天、D每隔4天各去一次，在2月份的最后一天，四人刚好都去了图书馆，那么从3月1日到12月31日只有一个人来图书馆的日子有____ 天.
9. 六年级六个班组织乒乓球单打比赛,每班派甲、乙两人参赛，根据规则每两人之间至多赛一场，且同班的两人之间不进行比赛.比赛若干场后发现,除一班队员甲以外,其他每人已比赛过的场数各不相同,那么一班队员乙已赛过____场.
10. 人的血型通常为A型,B型,O型,AB型.子女的血型与其父母血型间的关系如下表所示:
父母的血型 子女可能的血型
O,O O
O,A A,O
O,B B,O
O,AB A,B
A,A A,O
A,B A,B,AB,O
A,AB A,B,AB
B,B B,O
B,AB A,B,AB
AB,AB A,B,AB
现有三个分别身穿红,黄,蓝上衣的孩子,他们的血型依次为O,A,B.每个孩子的父母都戴着同颜色的帽子,颜色也分红,黄,蓝三种,依次表示所具有的血型为AB,A,O.那么穿红、黄、蓝上衣的孩子的父母戴帽子的颜色是 、 、 .
二、解答题
11. 刘毅、马宏明、张健三个男孩都有一个妹妹,六人在一起打乒乓球,进行男女混合双打,事先规定:兄妹不搭档.
第一盘:刘毅和小萍对张健和小英；第二盘:张健和小红对刘毅和马宏明的妹妹.小萍、小红和小英各是谁的妹妹？
12. 四位运动员分别来自北京、上海、浙江和吉林,在游泳、田径、乒乓球和足球四项运动中,每人只参加了一项,且四人的运动项目各个不相同,除此以外,只知道一些零碎情况：
(1)张明是球类运动员,不是南方人；
(2)胡老纯是南方人,不是球类运动员；
(3)李勇和北京运动员、乒乓球运动员三人同住一个房间；
(4)郑永禄不是北京运动员,年龄比吉林运动员和游泳运动员两人的年龄小；
(5)浙江运动员没有参加游泳比赛.
根据这些条件,请你分析一下:这四名运动员各来自什么地方?各参加什么运
动?
13. 老吴、老周、老杨分别是工程师、会计师和农艺师，还分别是业余作家、画家和音乐家,但不知道每人的职业及业余爱好,只知道：
(1)业余音乐家、作家常和老吴一起看电影；
(2)画家常请会计师讲经济学的道理；
(3)老周一点也不爱好文学；
(4)工程师埋怨自己对绘画、音乐一窍不通.
请你指出每个人的职业和爱好.
14. 四个人聚会,每人各带了2件礼品,分赠给其余三个人中的二人,试证明:
至少有两对人,每对人是互赠过礼品的.
———————————————答 案——————————————————————
1. C
A、C的预测截然相反,必一对一错.因为只有一人对,不论A、C谁对,B必
错,所以甲是最后一名,C对.
2. E
如右图,E坐在A、B之间.
3. 2,3.
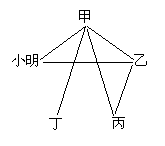由题意可画出比赛图,已赛过的两人之
间用线段引连(见右图).由图看出小明赛了2盘.因
为一共赛了六盘,共得12分,所以小明得了
12-(2+4+1+2)=3(分).
4. 三,丙,丁,甲,乙.
由刘的讲话,知这一天是星期三,刘要去丙单位.钱要去丁单位,曹去的是甲单位,洪去的是乙单位.
5. 埃及,8；法国，3；朝鲜，5；墨西哥，15.
容易知道,墨西哥人住得最高,埃及人次之,朝鲜人又次之,法国人最低,各层次分别15,8,5和3.由(2)知B是法国人,由(3)和D是墨西哥人,由(1)知A是埃及人,而C是朝鲜人.
6. 86240.
因为每人猜对两个数字,三人共猜对 张:842±1
2´3=6(个)数字,而电话号码只有5位, 王:26048
所以必有一位数字被两人同对猜对.如右 李:4980
图所示,猜对的是左起第三位数字2.因为每人猜对的两个数字不相邻,所以张、
李猜对的另一个数字分别在两端,推知王猜对的数字是6和4,进一步推知张猜对8,李猜对0.电话号码是86240.
7. 19735.
因为每个数字都有人猜对,所以每人至少猜对两个数字.下页右上图中,同一位数中只有方框中的两个数相同,如果每人猜对的数字多于两位,相同的数字至少有3´3-5=4(组),所以每人恰好猜对两个数字. 王: 9 3 7 1 5
三人共猜对2´3=6(个)数字,因为电话号码只有
张: 7 9 5 3 8
5位,所以相同的一组是正确的,即左起第四位是 李: 1 5 2 3 9
3.因为每人猜对的数字不相邻,所以张、李猜对的另一个数字都在前两位,王猜对的两个数字是7和5,进而推知张猜对9,李猜对1.电话号码是19735.
8. 51天.
因为[8,6,4]=24,所以四人去图书馆的情况每24天循环一次(见下表):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| D |
| C |
| A、B、D | |||
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| C、D |
|
|
| A、B、D | |||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
C | D |
|
|
| A、B、C、D |
每24天有4天只有1人去图书馆.3月1日至12月31日有306天,
306¸24=12…18，所以所求天数为4´12+3=51(天).
9. 5
根据题意,有11名队员比赛场数各不相同,并且每人最多比赛10场,所以除
甲外的11名队员比赛的场数分别为0~10.
已赛10场的队员与除已赛0场外的所有队员都赛过,所以已赛10场的队员
与已赛0场的队员同班；
已赛9场的队员与除已赛0、1场外的所有队员都赛过,所以已赛9场的队员与已赛1场的队员同班；
同理,已赛8、7、6场的队员分别与已赛2、3、4场的队员同班；所以甲与已赛5场的队员同班,即乙赛过5场.
注 本题可以求出甲也赛了5场,分别与已赛10、9、8、7、6场的队员各赛1场.
10. 蓝、黄、红.
解法一
题中表明,每个孩子的父母是同血型的.具有B型血的孩子,其父母同血型时,由表中可见,只能是B型或AB型,但题中没有同具B型血的父母,所以戴红帽子的父母的孩子穿蓝上衣.具有A型血的孩子的同血型的父母,只可能同为A型血或同为AB型血.今已知有一对父母为AB型血者,所以穿黄上衣的孩子的父母戴黄帽子.由表中可见,其孩子为O型血时,父母血型只能同为A型或B型或O型.今已知不具有同为B型血的父母,而同为A型血的父母的孩子已知具有A型血.把代表孩子的点与他的可能双亲的代表点之间连一直线段,便可得下面的图；由于孩子与其父母之间是唯一搭配的,所以,保存下来的只有连着红、蓝；黄，黄及蓝，红的三条边.
所以,穿红上衣(O型血)孩子的父母戴蓝帽子.
孩子衣服颜色 父母帽子颜色
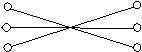(O型血)红
红(AB型血)
(A型血)黄 黄(A型血)
(B型血)蓝 蓝(O型血)
所以,穿红上衣的孩子的父母戴蓝帽子；穿黄上衣的孩子的父母戴黄帽子；穿蓝上衣的孩子的父母戴红帽子.
11.刘毅和小红,马宏明和小英,张健和小萍分别是兄妹.
| 萍 | 英 | 红 | |||||
|
| ´ | ||||||
| 马 | ´ | ||||||
| 张 | ´ | ´ | |||||
| 萍 | 英 | 红 |
| |||||
| 刘 | ´ | ´ | √ |
| ||||
| 马 | ´ | √ | ´ |
| ||||
| 张 | √ | ´ | ´ |
| ||||
刘
12.用表格解如下:
| 北 | 上 | 浙 | 吉 | 游 | 田 | 乒 | 足 | |
| ´ | ´ | 张 | ´ | ´ | ||||
| ´ | ´ | 胡 | ´ | ´ | ||||
| ´ | 李 | ´ | ||||||
| ´ | ´ | 郑 | ´ |
| 北 | 上 | 浙 | 吉 | 游 | 田 | 乒 | 足 | |||
|
| ´ | ´ | ´ | 张 | ´ | ´ | ||||
|
| ´ | 胡 | ´ | ´ | ||||||
| ´ | ´ | ´ | √ | 李 | ´ | |||||
| ´ | ´ | 郑 | ´ |
´
| 北 | 上 | 浙 | 吉 | 游 | 田 | 乒 | 足 | |||
|
| ´ | ´ | ´ | 张 | ´ | ´ | ´ | √ | ||
|
| ´ | 胡 | ´ | ´ | ||||||
| ´ | ´ | ´ | √ | 李 | ´ | ´ | ||||
| ´ | ´ | 郑 | ´ | ´ | √ | ´ |
´
|
| 上 | 浙 | 吉 | 游 | 田 | 乒 | 足 | |||
| √ | ´ | ´ | ´ | 张 | ´ | ´ | ´ | √ | ||
|
| ´ | 胡 | √ | ´ | ´ | ´ | ||||
| ´ | ´ | ´ | √ | 李 | ´ | √ | ´ | ´ | ||
| ´ | ´ | 郑 | ´ | ´ | √ | ´ |
´
| 北 | 上 | 浙 | 吉 | 游 | 田 | 乒 | 足 | |||
| √ | ´ | ´ | ´ | 张 | ´ | ´ | ´ | √ | ||
|
| √ | ´ | ´ | 胡 | √ | ´ | ´ | ´ | ||
| ´ | ´ | ´ | √ | 李 | ´ | √ | ´ | ´ | ||
| ´ | ´ | √ | ´ | 郑 | ´ | ´ | √ | ´ |
13.表解如下:
| 工 | 会 | 农 | 作 | 画 | 音 | |
| 吴 | ´ | ´ | ||||
| 周 | ´ | |||||
| 杨 |
|
| 会 | 农 | 作 | 画 | 音 | |||
|
| ´ | 吴 | ´ | √ | ´ | |||
| ´ | 周 | ´ | ´ | √ | ||||
| 杨 | √ | ´ | ´ |
´
|
| 会 | 农 | 作 | 画 | 音 | |||
|
| ´ | √ | 吴 | ´ | √ | ´ | ||
| ´ | √ | ´ | 周 | ´ | ´ | √ | ||
| √ | ´ | ´ | 杨 | √ | ´ | ´ |
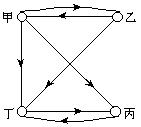
´14. 设此四人为甲、乙、丙、丁并用画在平面上的四个点分别表示他们，称为它们的代表点,当某人(例如甲)赠了1件礼品给另一个(例如乙)时,就由甲向乙的代表点画一条有指向的线,无非有以下两个可能:
(1)甲、乙、丙、丁每人各收到了2件礼品.
(2)上面的情形不发生.这时只有以下一个可能,即有一个人接受了3件礼品
(即多于2件礼品；因为一人之外总共还有三个人，所以至多收到3件礼品).(或许会有人说,还有两个可能:有人只收到1件礼品及有人什么礼品也没收到.其实,这都可归以“有一人接受了3件礼品”这个情形.因为,当有一人(例如甲)只接受了1件礼品的情形发生时,四人共带来的8件礼品中还剩下7件在甲以外的三个人中分配,如果他们每人至多只收到2件礼品,则收受礼品数将不超过6件,这不可能,所以至少有一人收到2件以上(即3件)礼品,同样,当甲未收到礼品时,8件礼品分给乙、丙、丁三人，也必定有人收到3件礼品).
当(1)发生时,例如甲收到乙、丙的礼品,由于甲发出的礼品中至少有1件给了乙或丙,为确切计,设乙收到了甲的礼品,于是我们先有了一对人:(甲、乙),他们互赠了礼品，如果丙也收到甲的礼品,那么又有了第二对互赠了礼品的人(甲、丙)；如果收到甲礼品的另一人是丁(如右图)丁的2件礼品必定分赠了乙及丙(甲已收足了本情形中限定的2件礼品)丙或乙的另一件礼品给了丁,则问题也解决(这时另一对互赠了礼品的人便是(乙、丁)或(丙、丁)但丙的另一件礼品只能给丁,因为这时乙已收足了2件礼品,所以，当本情形发生时,至少能找到两对互赠过1件礼品的人.
当(2)发生时,不失一般性,设甲收到了来自乙、丙、丁的各1件礼品，但甲又应向他们之中的某两人(例如乙、丙)各赠送1件礼品,于是(甲、乙),(甲、丙)便是要找的两对人.总上可知,证明完毕.
 |