33、不等式的应用（3）
一、典型例题
1、
若a>0,0<b<1且
，求x的取值范围。
2、
若
，求a的取值范围。
3、
已知正数x,y满足x+2y=1，求
的最小值。
4、
已知函数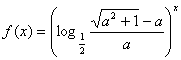
在R上为减函数，求实数a的取值范围。
5、 已知关于x的方程loga(x-3)+1=log2(x+2)+loga(x-1)有实根，求实数a的取值范围。
6、 已知函数f(x)=ax2+bx+c(a>b>c)满足f(1)=0，又函数f(x)图象上有两点P1(x1,f(x1)), P2(x2,f(x2))满足a2+(f(x1)+f(x2))a+f(x1)f(x2)=0，求证：b≥0 。
7、 设函数f(x)=ax2+bx+c对一切x∈[-1,1]，都有f(x)≤1，求证：对于一切x∈[-1,1]，都有2ax+b≤4。
8、 定义在（-1，1）上的奇函数f(x)在整个定义域上是减函数，且f(1-a)+f(1-a2)<0，求实数a的取值范围。
9、
已知函数f(x)在（-∞，+∞）上单调递减，且满足f(x+y)=f(x)f(y),f(2)=
，求使得f(x)f(3x-1)<
成立的x的取值范围。
10、 一造纸厂排出的污水，今年起若不经过处理，该厂将受环保部门的处罚，第一个月罚款3千元，以后每月递增2千元，原生产总收入f(n)是生产月份的一次函数，且生产一个月总收入7万元，生产三个月的总收入21万元。如果该厂投资40万元治理污水，将不受罚，收入逐月增长，且总收入g(x)是生产月份n的二次函数（不含常数项）。生产一个月总收入10.1万元，生产二个月总收入20.4万元，问经过多少个月，投资就开始见效（即生产总收入与投资额的差不小于生产总收入f(n)与罚款总额的差）。
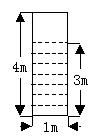
11、 如图，一矩形闸门宽1m、长4m、水深3m，由于压强随水深而变化，不得已求近似值，将闸门沿水深的方向分为n等份，其每一层所受的压强（单位：t/m2）如下表所示：已知闸门能永久承受的压力为5 t，试问使用此闸门是否安全，并说明理由。
| 层序 | 不足近似值 | 过剩近似值 |
| 最上一层 | 0 |
|
| 第二层 |
|
|
| 第三层 |
|
|
| …… | …… | …… |
| 第n层 |
|
|
