数（三）
——二次函数
1、 某文具店出售书包和文具盒，书包每个定价30元，文具盒每个定价5元，该店制定了两种优惠方案：①买一个书包赠送一个文具盒。②按总价九折付款。某班需购8个书包，文具盒若干（不少于8个）如果设购文具盒数为x（个），付款为y（元）；
（1） 分别求出两种优惠方案中y与x之间的函数关系式；
（2） 若购文具盒60个，两种方案中哪一个更省钱？
2、
已知抛物线y=
和直线y=ax+1
（1） 求证：不论a取何值，抛物线与直线必有两个不同的交点；
（2）
设A（x1，y1）、B（x2，y2）是抛物线与直线的两个交点，点P为线段AB的中点，且点P的横坐标为
，试用a表示点P的纵坐标；
（3）
函数A、B两点的距离
，试用a表示d。
3、
如图在直角坐标系xoy中，二次函数图象的顶点坐标为C（4，
），且在x轴上截得的线段长为6。
（1） 求二次函数的解析式。
（2）
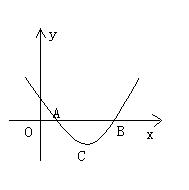在x轴上方的抛物线上，是否存在点Q，使得以Q、A、B三点为顶点的三角形与△ABC相似；如果存在，请求出Q点的坐标；如果不存在，请说明理由。
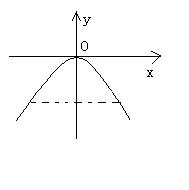
4、 有一座抛物线形拱桥，正常水位时桥下面宽度为20米，拱顶距离水面4米；
（1） 在如图所示的直角坐标系中，求出该抛物线的解析式；
（2） 在正常水位的基础上，当水位上升h（米）时，桥下水面的宽度为d（米）。试求出将d表示为h的函数解析式。
（3） 设正常水位时桥下的水深为2米，为了保证过往船只顺利航行，桥下水面的宽度不得小于18米，求水深超过多少米时就会影响过往船只在桥下顺利航行？
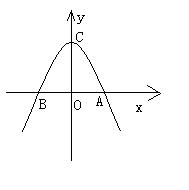
5、
如图已知抛物线
与x轴有两个交点A、B，点A在x轴的正半轴上，点B在x轴的负半轴上，且OA=OB。（1）求m的值；（2）求抛物线的解析式，并写出抛物线的对称轴和顶点C的坐标；（3）问在抛物线上是否存在一点M，使△MAC≌△OAC，若存在，求出点M的坐标；若不存在，请说明理由。
6、
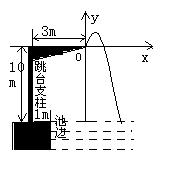某跳水运动员进行10米跳台跳水训练时，身体（看成一点）在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线（图中标出的数据为已知条件）。要跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面
米，入水处距池边的距离为4米，同时，运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误，（1）求这条抛物线的解析式；（2）在某次试跳中，测得运动员在空中运动路线是如图抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为
米，问此次跳水会不会失误？并通过计算说明理由。
7、 如图，已知矩形ABCD的边长AB=3，AD=2，将此矩形置于直角坐标系xoy中，使AB在x轴上，点C在直线上y=x－2。（1）按题设画出图形，并求出矩形的顶点A、B、C、D的坐标；（2）若直线y=x－2与y轴交于点E，抛物线y=ax2+bx+c过E、A、B三点，求抛物线的解析式；（3）判断上述抛物线的顶点是否落在矩形ABCD的内部？并说明理由。
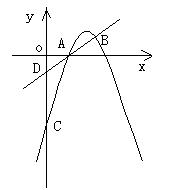8、如图，已知抛物线y=－x2－（m－4）x+3（m－1）与x轴交于A、B两点，与y轴交于C点（1）求m的取值范围；（2）若m<0，直线y=－
x－1经过点A，与y轴交于点D，且AD·BD=
，求抛物线的解析式；（3）若A点在B点左边，在第一象限内（2）中所得的抛物线上是否存在一点P，使直线PA平分△ACD的面积？若存在，求出P点的坐标；若不存在，说明理由。