第二章 二次方程(一)(2.1~2.4)
姓名 班级 学号
一、填空题(每小题3分,共24分)
1、解简单高次方程的基本思路是 ,具体方法有:⑴因式分解法;⑵ .
2、方程![]() 的根是
.
的根是
.
3、方程![]() 的根是
. 4、方程
的根是
. 4、方程![]() 的根是
.
的根是
.
5、方程![]() 有实数根,则k的取值范围是
.
有实数根,则k的取值范围是
.
6、用换元法解方程![]() ,设
,设![]() ,则原方程可变形为
.
,则原方程可变形为
.
7、若![]() ,则
,则![]() .
.
8、![]() ,
,![]() ,
,![]() 是一三角形的三边长,若方程组
是一三角形的三边长,若方程组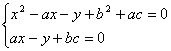 只有一组解,则这个三角形是
三角形.
只有一组解,则这个三角形是
三角形.
二、选择题(每小题4分,共32分)
9、关于方程![]() ,下列说法错误的是( )
,下列说法错误的是( )
A、是一元高次方程; B、是双二次方程; C、方程有四个不同的实根 D、方程可用换元法解.
10、下列关于![]() 的方程属于根式方程的是( )
的方程属于根式方程的是( )
A、![]() ; B、
; B、![]() ; C、
; C、![]() ; D、
; D、![]() .
.
11、方程![]() 的根是( )
的根是( )
A、不存在; B、![]() C、
C、![]() D、
D、![]()
12、方程![]() 的解是( )
的解是( )
A、![]() B、
B、![]() C、
C、![]() D、无解
D、无解
13、方程组![]() 的解是( )
的解是( )
A、![]() B、
B、![]() C、
C、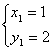
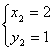 D、以上答案都不对
D、以上答案都不对
14、下列方程中,有实数解的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
15、利用换元法把方程![]() 化为整式方程,正确的是( )
化为整式方程,正确的是( )
A、设![]() B、设
B、设![]()
C、设![]() D、设
D、设![]()
16、关于![]() 的方程
的方程![]() 的根为( )
的根为( )
A、![]() ;B、x1=k+1,x2=k-1; C、x1=k,x2=k=1; D、
;B、x1=k+1,x2=k-1; C、x1=k,x2=k=1; D、![]()
三、解答题(共44分)
17、解下列方程或方程组(第⑴⑵⑶小题每题7分,第⑷题满分14分)
⑴![]() ;
⑵
;
⑵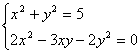
⑶![]() ⑷
⑷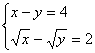
18、已知![]() ,
,![]() 是方程
是方程![]() 的两个解,求
的两个解,求![]() ,
,![]() 的值.(本题9分)
的值.(本题9分)
四、提高题(共20分)
19、解方程![]()
20、已知关于![]() 的方程
的方程![]() 的一个根是
的一个根是![]() ,试解这个方程.
,试解这个方程.
21、先阅读下面方程x+![]() =2的过程,然后填空。解:(第一步)将方程整理为x-2+
=2的过程,然后填空。解:(第一步)将方程整理为x-2+![]() =0;(第二步)设y=
=0;(第二步)设y=![]() ,原方程可化为y2+y=0;(第三步)解这个方程得:y1=0,y2=-1;(第四步)当y=0时,
,原方程可化为y2+y=0;(第三步)解这个方程得:y1=0,y2=-1;(第四步)当y=0时,![]() =0,解得x=2,当y=-1时,
=0,解得x=2,当y=-1时,![]() =-1,方程无解;(第五步)∴x=2是方程的解。
=-1,方程无解;(第五步)∴x=2是方程的解。
在以上解题过程中,第二步用的方法是 ;第四步中,判定方程![]() =-1无解的根据是 ;上述解题过程不完整,缺少的一步是
。
=-1无解的根据是 ;上述解题过程不完整,缺少的一步是
。