初二数学阶段性测试
一、填空（每空2分，共44分）
1．点C在线段AB上，AC∶CB=3∶4，则AB∶CB= 。
2．在比例尺1∶的地图上，量得太原到北京的距离为6.4厘米，则太原到北京的实际距离为 公里。
3．已知：
，
，
，
是成比例线段，其中=3cm ，=2cm，
=6cm，则= cm。
4．已知：
，则
；
。
5．已知
，则
。
6．已知如图，D是△ABC的AB边上一点，要使△ABC∽△ACD
则还须具备一个条件是__ __.或 。
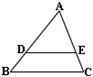7．如图，已知△ADE∽△ABC，AD=6cm，DB=3cm，BC=9.9cm, ∠B=50°,
则∠ADE= ，DE = cm。
8、一个四边形的边长分别是3，4，5，6，另一个与它相似
的四边形最小边长为6，则另一个四边形的周长是______________.
9．数据2，2，3，4，4的方差S2 = 。
10．为了了解某校初中毕业生的身高情况，从各班中抽取了20名学生测量身高，在这个问题中，总体是 ；个体是 。
样本是 。
11．命题“相等的角是对顶角”的条件是 ，
结论是
。
12．在△ABC中，∠A=∠B=2∠C，则∠A= ∠C= 。
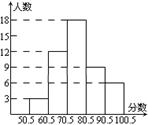
13．某地区为了增强市民的法制观念，抽调了一部分市民进行了一次知识竞赛，竞赛成绩(得分取整数)进行整理后分成五组，并绘制成频数分布直方图，请结合直方图提供的信息填空
(1)抽取了 人参赛。
(2)60.5~70.5这一分数段的频数是 、 频率是 。
二、选择题（每题3分，共27分）
1．在相同时刻的物高与影长成比例，如果高为1.5米的测竿的影长为2.5米，那么影长为30米的旗杆的高是（ ）
A.20米 .B.18米 C.16米 D.15米
2．在矩形ABCD中，E、F分别是CD、BC上的点， 若∠AEF=90°，
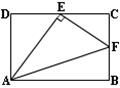则一定有 （ ）
(A)ΔADE∽ΔAEF (B)ΔECF∽ΔAEF
(C)ΔADE∽ΔECF (D)ΔAEF∽ΔABF
3．如图，在△ABC中，M、E把AC边三等分，MN∥EF∥BC，MN、EF把△ABC分成三部分，则自上而下部分的面积比为 （ ）
A 1∶1∶1 B 1∶2∶3 C 1∶4∶9 D 1∶3∶5
4．为了判断甲、乙两个小组学生英语口语测验成绩哪一组比较整齐，通常需要知道两组成绩的（ ）
A.平均数 B.方差 C.众数 D.频率分布
5、某校初中三年级共有学生400人，为了解这些学生的视力情况，抽查了20名学生的视力，对所得数据进行整理.在得到的频数分布表中，若数据在0.95~1.15这一小组频率为0.3，则可估计该校初中三年级学生视力在0.95~1.15范围内的人数约为 （ ）
A.6人 B.30人 C.60人 D.120人
6．下列句子中，①动物都需要水 ②
美丽的天空 ③
如果>，>，
那么= ④
过直线
外一点作的平行线 是命题有 （ ）
A 1个
B 2 个 C 3 个 D 4个
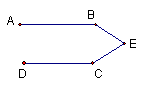
7．如图，AB∥CD，∠C=110°，∠B=120°，则∠BEC= （ ）
A 110° B 120° C 130° D 150°
8．如图，下列哪种说法是错误的 （ ）
A ∠B >∠ACD B ∠B+∠ACB =180°-∠A
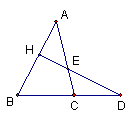C
∠B+∠ACB < 180°
D ∠HEC>∠B
9．下列说法正确的是 （ ）
A 相等的角是对顶角 B 同位角相等
C 三角形的外角大于内角
D 若∥,∥,则∥
三、解答题
1．.为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分取整数，满分为100分)进行统计.（8分）
（1）请你根据所学知识补全表格 （2）绘制频数分布直方图
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 | 1.00 |
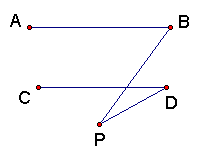
2．已知：如图，AB∥CD 试猜想 ∠B、∠D、∠P有什么关系
并证明你的猜想。（8分）
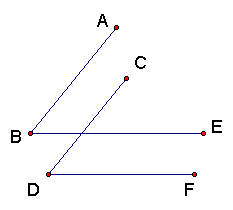
3．已知：如图 AB∥CD ∠ABE = ∠CDF
求证： BE∥DF （8分）
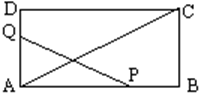
4．如图，在矩形ABCD中,AB=12cm，BC=6cm, 点P沿AB边从点A开始向点B以2cm/秒的速度移动，点Q沿DA边从点D开始向点A以1cm/秒的速度移动，如果P、Q同时出发，用t（秒）表示运动时间(0≤t≤6), 那么当t为何值时，
以Q、A、P为顶点的三角形与△ABC相似？（5分）
