八年级(上)数学单元目标检测题(A)

八年级(上)数学单元目标检测题(A)

　　　　　　　　　　　　　　   (四边形性质探索)

姓名:　　　　　   班别:　　　　  : 座号:　　　　  评分:　　　　　

一、　　　　　  选择题( 本大共8小题, 每小题3分,共24分)

1.　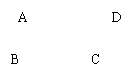　　如图, 在平行四边形ABCD中, ∠B=60^o，AB=5cm，则下面正确的是（ ）

A．BC=5cm，∠D=60^o　　 B. ∠C=120^o, CD=5cm　　　

C．AD=5cm, ∠A=60^o　　 D. ∠A=120^o, AD=5cm

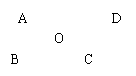
2.　　　如图, AC, BD是平行四边形ABCD的对角线, AC与

 BD交于点O, AC=4, BD=5, BC=3, 则△BOC的周长(　)　 A．7.5　　 B. 12　　C. 6.　 D. 无法确定.

3.　　　下面说法正确的是(　)

A. 一组对边相等且平行的四边形是平行四边形

　　　B. 有两边相等的四边形是平行四边形

C.　四个全等的三角形一定可组成一个平行四边形

D.　一组对边平行, 另一组对边相等的四边形是平行四边形　　　　　 　　　

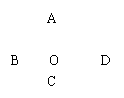4. 如图, AC, BD是菱形ABCD的对角线, 且交于点O,

则下面正确的是(　)

A. 图中共有8个三角形, 它们不全等.

B. 图中只有四个全等的直角三角形

C. 图中有四对不是直角的全等三角形

D. 图中有四个全等的直角三角形, 两对全等的等腰三角形

5. 铺设地板的60×60规格的瓷砖的形状是(　)

A. 矩形　　　　 B. 菱形　　　　 C. 正方形　　　　 D. 梯形.

6. 一正多边形的每个外角都是30^o, 则这个多边形是(  )

A. 正方形　　　 B. 正六边形　　 C. 正八边形　　　 D. 正十二边形.

7. 下面给出的图形能密铺的是(  )

A. 正五边形　　　B. 三角形　　　C. 正十边形　　　 D. 正十二边形.

8. 一矩形两对角线之间的夹角有一个是60^o, 且这角所对的边长5cm,则对角线长为(　)　 A. 5 cm　　 B. 1ocm　　　C. 5cm　　　D. 无法确定

二、　填空题(本大题共6小题,每小题4分,共24分)　　

9. 如图, AB和CD是夹在两平行线之间的平行

线段,则AB　　CD(填“”或“”或“=”)

10．如图，E、F、G、H分别是　ABCD

各边的中点，则图中有　 个平行四边形。

11．一个矩形的对角线长1ocm，一边长6cm，

则其周长是　　　　，面积是　　　 。

12．在梯形ABCD中，AD∥BC，AB=CD，

直线DE∥AB, DE把梯形分成两个图形，

一个是　　　 ，另一个是　　　　。

13．十边形的内角和是　　　　  度。

14．若两种正多边形组合能密铺，则这两种正多边形可以是　　　　　 。

三、 解答题（本大题共7小题，共52分）

15．将一个三角形经过怎样的旋转能得到一个平行四边形？并说说你的理由。（7分）

16．一菱形周长为20cm, 其一对角线长6cm，求其另一对角线的长。（7分）

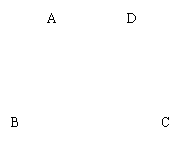
17．如图，在梯形ABCD中，AD∥BC，∠B=90^o，

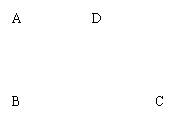AD=AB=2，且BD=CD，求△DBC的周长和梯形

ABCD的面积。（8分）

18．小明家准备在客厅铺设地板砖.客厅地面是一个矩形, 长6.3米, 宽4.8米. 装修工人提出两个建议, 一是铺设80cm×80cm的地板砖, 每块4o元;

二是铺设60cm×60cm的地板砖, 每块25元. 小明要求材料费少, 又铺得整齐为好, 你能帮他出个好主意吗?(8分)

19. 如图是一个正方形的花坛, 边长为10米. 在花坛上建两条相互垂直的小道, 把花坛分为四个面积相等的部分, 小道宽1米. 问面积相等的部分各为多少?(7分)

2o. 如图, 梯形ABCD, AD∥BC, AB=CD, AC和BD是梯形的两条对角线,那么这两条对角线是否相等? 说说你的理由.(7分)

　 21. 在所学过的线段、角、三角形、平行四边形、菱形、矩形、正方形、等腰梯形、正五边形、正六边形等图形中，你认为哪些图形是轴对称图形，哪些图形是中心对称图形，哪些图形既是轴对称又是中心对称图形？说说你的理由，并指出它们的对称轴或对称中心。（8分）

八年级(上)数学单元目标检测题(B)

　　　　　　　　　　　　　　　 (四边形性质探索)

姓名:　　　　　   班别:　　　　  : 座号:　　　　  评分:　　　　　

一、选择题( 本大共6小题, 每小题4分,共24分)

　1．下面说法正确的是(　)

　A. 一个三角形经过适当的旋转得到的图形和原图形可组成平行四边形.

　B. 一个三角形经过适当的平移, 前后图形可组成平行四边形.

　C. 因为正方形也可以看作菱形, 故菱形经过适当的旋转可得到正方形.

　D. 夹在两平行直线之间的线段相等.

　2. 当矩形的对角线互相垂直时, 矩形变成(　)

　A. 菱形　　　　 B. 等腰梯形　　　　C. 正方形　　　 D. 无法确定

　3. 已知正方形的边长为4cm, 则其对角线长(　)

　A. 8cm　　　　  B. 16cm　　　　　  C. 32cm　　　　 D. 4cm

　4. 一个多边形, 它的每个内角都等于相邻外角的5倍, 则这个多边形是(　)

　A. 正五边形　 　B. 正十边形　　　　C.正十二边形　　D. 不存在

　5. 下面图形是一个中心对称图形的是(　)

　A. 三角形　　　 B. 等腰梯形　　　　C.平行四边形　　D. 正五边形

　6. 一等腰梯形的腰长13cm, 两底差为1ocm, 则其高为(　)

　A. cm　　　 B. 12cm　　　　　  C. 69cm　　　　 D. 144cm

二、 填空题(本大题共6小题,每小题4分,共24分)  

　7. 夹在两条平行直线之间的平行线段的大小关系是　　　　.

　8. 已知菱形的两条对角线的长分别是6cm和8cm, 则其周长为　 ,面积为　.   

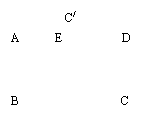
　9. 当菱形的对角形长相等时, 它变成了　　　图形.

　10.如图, 把矩形ABCD沿直线BD折叠, 使点C落

在C^/处, BC^/交AD于E, AD=8,AB=6, 则点E到BD

的距离是　　　　.

　11. 当两个多边形相差一条边, 则它们内角和相

　差　　 度, 外角和又相差　　 度.

　12. 如图, 一直角梯形ABCD, AD∥BC, ∠B=90^o,

　且腰AB=5, 两底差为12, 则另一腰CD=　　  .

三、 解答题（本大题共7小题，共52分）

　13.如图, 在平行四边形ABCD中,E、F是对角线AC

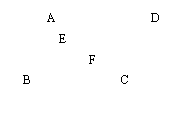　上的点, 且AE=CF, 则四边形EBFD是平行四边形　　

　吗? 说说你的理由.(7分)

　14.小红的房门做好了, 现要检测这房门是否成　　　

　矩形, 你有什么办法帮他吗? 说说看.(7分)

　 15. 如图, 0是正方形ABCD内一点, 且到各顶点距离相等, 都等于3, 你能

　 求这个正方形的面积吗? 试试看.

　 16. 已知梯形ABCD, AD∥BC, AB=CD, ∠B=60^o,

　 且AD=5, BC=13, 求梯形的腰长和其他三个角

　 的度数.(7分)

　 17. 观察下面图形, 并回答问题.

　①四边形、五边形、六边形各有几条对角线？从中得到什么规律？

②根据规律求七边形的对角线的数量。

③n边形的对角线的数量呢？（8分）

　18．密铺可组成许多漂亮的图案，你认为哪些多边形及其组合可以密铺？并说

　说理由。（7）

　19．探索下列问题：（9）

①菱形或正方形的对角线互相垂直，那么对角线互相垂直的四边形一定是菱形

或正方形吗？举例说明（可画图表示）。

②长度一定的铁线围成什么样的平行四边形的面积最大？说说你的理由。

　③一个矩形绕其对角线交点旋转至少多大的角度才与原来图形重合？梯形呢？

试题略解:

(A)卷

一、1. B  2. A　3. A　4. D　5. C　6. D　7. B　8. B

二、9. =　 1o. 9　 11. 28cm,48cm²　 12. 平行四边形,等腰三角形　

　　13. 144o　　 14. 正三角形和正方形

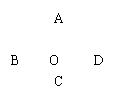三、15.绕三角形一边中点旋转180^o. 因为旋转图形的形状、大小不变,再根据两组对边相等的四边形是平行四边形.

　　16.如图,AC=6cm,AB=20÷4=5(cm),

在Rt△AOB中,BO==4,BD=2×4=8.

所以菱形另一对角线长8cm.

17.在Rt△ABD中,BD==CD,Rt△BDC中,

BC=,△BDC的周长=2,

梯形ABCD的面积=2(2+4)÷2=6.

18.在矩形的长的一边用80×80规格的不到8块,但要取8块才铺得整齐,宽的一边刚好6块,共8×6=48块,需要48×40=192(元); 若用60×60规格的在长的一边要10块半,宽的一边要8块,共10.5×8=84块,需要84×25

=2100(元),故用80×80规格的好.

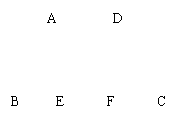19.[10²-2×1×10+1×1]÷4=20.25(米²).

2o.两对角线相等.理由是:作AE⊥BC于E,

DF⊥BC于F, △ABE≌△DCF,∠ABE=∠DCF,

△ABC≌△DBC, AC=BD.

21. 线段、角、等腰三角形、菱形、矩形、

正方形、等腰梯形、正五边形、正六边形

都是轴对称图形；线段、平行四边形、菱形、矩形、正方形、正六边形是中心对称图形；线段、菱形、矩形、正方形、正六边形既是轴对称图形又是中心对称图形。（理由略）

（B）卷

一、1. A　　2. C　　3. D　　4. C　　5. C　　6. B

二、 7. 相等　　8. 20cm,24cm²　　 9. 正方形　　  10. 　　 

11. 180, 0　　 12. 13

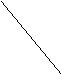
三、13.四边形EBFD是平行四边形.理由是:

连接BD与AC交于点O,因为AE=CF, 所以OE=OF,又BO=DO, 故四边形EBFD是平行四边形.

14.可以量四个角是否直角,或对角线是否互相平分且相等,

或两组对边相等及有一个角是直角等等.

15.连接AC和BD,则点O是这两对角线的交点, 正方形面积

AB²=3²+3²=18.

16.作DE∥AB交BC于E, 梯形的腰AB=CD=EC=13-5=8, ∠C=∠B=60^o,

∠A=∠D=120^o.

17.①四边形有2条对角线,五边形有5条对角线,六边形有9条对角线.

2=, 5=, 9=,…

②七边形的对角线有: 条.

③n边形的对角线有:条.

18.三角形、四边形、正六边形或三角形与正四边形、正三角形与正六边形、

正四边形与正六边形、正十二边形的组合可以密铺。（理由略）

19．①不一定，如图，

②正方形最大。（理由略）

③矩形的是180^o，梯形的是

360^o。