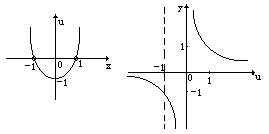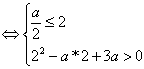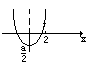一、复合函数
函数y=log2x是对数函数,那么函数y=log2(2x-1)是什么函数呢?我们可以这样理解:
设y=log2u,u=2x-1,因此函数y=log2(2x-1)是由对数函数y=log2u和一次函数u=2x-1经
过复合而成的。
一般地,如果y是u的函数,而u又是x的函数,即y=f(u),u=g(x),那么y关于x的函
数y=f[g(x)]叫做函数f和g的复合函数,u叫做中间变量。
例1.已知f(x)=x+,g(x)=x2-2,求f[g(x)]和g[f(x)]的解析式。
解:f[g(x)]=f(x2-2)=(x2-2)+;
g[f(x)]=g(x+)=(x+
)2-2=x2+
。
例2.已知f(x)的定义域为[0,4],求函数f(x2)的定义域。
解:f(x2)可以看作ψ(x)=f[g(x)],其中u=g(x)=x2,则f(x2)=f(u),即ψ(x)=f(u)。
由已知f(u)的定义域为[0,4],即0≤u≤4,所以0≤x2≤4,解得-2≤x≤2。
∵ 函数f(x2)的定义域为[-2,2]。
例3.求函数y=的值域。
分析:令u=x2-1,y=,函数y=
的定义域为x≠±1,分别作出函数u=x2-1,
y=的图象。
由x≠±1→u≥-1,且u≠0,→y>0,或y≤-1。
故函数y=的值域为(-∞,-1]∪(0,+∞)。
二、复合函数的单调性。
定理:设y=f(u),u=g(x),已知u=g(x)在[a,b]上是单调增(减)函数,y=f(u)在区
间[g(a),g(b)](或[g(b),g(a)]上是单调增(减)函数,那么复合函数y=f[g(x)]在[a,b]
上一定是单调函数,并有以下结论:
| u=g(x) | 增函数 | 增函数 | 减函数 | 减函数 |
| y=f(u) | 增函数 | 减函数 | 增函数 | 减函数 |
| y=f[g(x)] | 增函数 | 减函数 | 减函数 | 增函数 |
判断复合函数的单调性的步骤如下:(1)求复合函数定义域;(2)将复合函数分解为若干
个常见函数(一次、二次、幂、指、对函数);(3)判断每个常见函数的单调性;(4)将中间
变量的取值范围转化为自变量的取值范围;(5)求出复合函数的单调性。
例4.讨论函数y=0.8x2-4x+3的单调性。
解:函数定义域为R。
令u=x2-4x+3,y=0.8u。
指数函数y=0.8u在(-∞,+∞)上是减函数,
u=x2-4x+3在(-∞,2]上是减函数,在[2,+∞)上是增函数,
∴ 函数y=0.8x2-4x+3在(-∞,2]上是增函数,在[2,+∞)上是减函数。
这里没有第四步,因为中间变量允许的取值范围是R,无需转化为自变量的取值范围。
例5.讨论函数y=(log2x)2+log2x的单调性。
解:显然函数定义域为(0,+∞)。
令 u=log2x,y=u2+u
∵ u=log2x在(0,+∞)上是增函数,
y=u2+u在(-∞,-]上是减函数,在[-
,+∞)上是增函数(注意(-∞,-
]及
[-,+∞)是u的取值范围)
因为u≤-log2x≤-
0<x≤
,(u≥-
log2x≥-
x≥
)
所以y=(log2x)2+log2x在(0,]上是减函数,在[
,+∞)上是增函数。
三、利用复合函数求参数取值范围。
求参数的取值范围是一类重要问题,解题关键是建立关于这个参数的不等式组,必须
将已知的所有条件加以转化。
例6.已知函数f(x)=(x2-ax+3a)在区间[2,+∞)上是减函数,则实数a的取值范
围是_______。
分析如下:
令u=x2-ax+3a,y=u。
因为y=u在(0,+∞)上是减函数
∴ f(x)=(x2-ax+3a)在[2,+∞)上是减函数
u=x2-ax+3a在[2,+∞)上是增函数,且对任意x∈[2,+∞),都有u>0。
对称轴x=
在2的左侧或过(2,0)点,且u(2)>0。
|
|
|
-4<a≤4
例7.若f(x)=loga(3-ax)在[0,1]上是减函数,则a的取值范围是_______。
令u=-ax+3>0,y=logau,由于a作对数的底数,所以a>0且a≠1,由u=-ax+3>0得x<。
在[0,1]上,且u是减函数。
∴ f(x)=loga(3-ax)在[0,1]上是减函数。
y=logau是增函数,且[0,1]
(-∞,
]
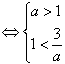
1<a<3
所以a的取值范围是(1,3)。
习题
1.函数y=在区间[4,5]上的最大值是_______,
最小值是_______。
2.函数y=(2-x-x2)的单调减区间是_______。
答案:
1.;1。
2.(-2,-)。