初二几何全等三角形检测
姓名：
一、填空题：
1、在△ABC中，若AC＞BC＞AB，且△DEF≌△ABC，则△DEF三边的关系为＿＿＿＜＿＿＿＜＿＿＿。
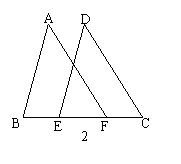2、如图1，AD⊥BC，D为BC的中点，则△ABD≌＿＿＿，△ABC是＿＿＿三角形。
3、如图2，若AB＝DE，BE＝CF，要证△ABF≌△DEC，需补充条件＿＿＿＿或＿＿＿＿。
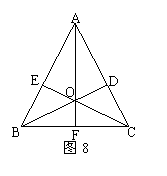
4、如图3，已知AB∥CD，AD∥BC，E、F是BD上两点，且BF＝DE，则图中共有＿＿＿对全等三角形，它们分别是＿＿＿＿＿。
 |
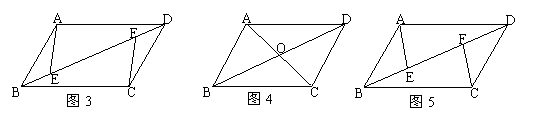5、如图4，四边形ABCD的对角线相交于O点，且有AB∥DC，AD∥BC，则图中有＿＿＿对全等三角形。
6、如图5，已知AB＝DC，AD＝BC，E、F在DB上两点且BF＝DE，若∠AEB＝120°，∠ADB＝30°，则∠BCF＝＿＿＿＿。
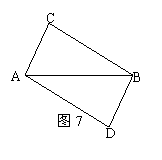
7、如图6，AE＝AF，AB＝AC，∠A＝60°，∠B＝24°，则∠BOC＝＿＿＿＿。
8、在等腰△ABC中，AB＝AC＝14cm，E为AB中点，DE⊥AB于E，交AC于D，若△BDC的周长为24cm，则底边BC＝＿＿＿＿。
9、若△ABC≌△A′B′C′，AD和A′D′分别是对应边BC和B′C′的高，则△ABD≌△A′B′D′，理由是＿＿＿＿＿＿，从而AD＝A′D′，这说明全等三角形＿＿＿＿相等。
10、在Rt△ABC中，∠C＝90°，∠A、∠B的平分线相交于O，则∠AOB＝＿＿＿＿。
二、选择题：
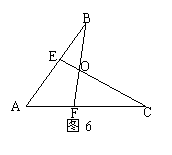
11、如图7，△ABC≌△BAD，A和B、C和D分别是对应顶点，若AB＝6cm，AC＝4cm，BC＝5cm，则AD的长为（ ）
A、4cm B、5cm C、6cm D、以上都不对
12、下列说法正确的是（ ）
A、周长相等的两个三角形全等
B、有两边和其中一边的对角对应相等的两个三角形全等
C、面积相等的两个三角形全等
D、有两角和其中一角的对边对应相等的两个三角形全等
13、在△ABC中，∠B＝∠C，与△ABC全等的三角形有一个角是100°，那么在△ABC中与这100°角对应相等的角是（ ）
A、∠A B、∠B C、∠C D、∠B或∠C
14、下列条件中，能判定△ABC≌△DEF的是（ ）
A、AB＝DE，BC＝ED，∠A＝∠D
B、∠A＝∠D，∠C＝∠F，AC＝EF
C、∠B＝∠E，∠A＝∠D，AC＝EF
D、∠B＝∠E，∠A＝∠D，AB＝DE
15、AD是△ABC中BC边上的中线，若AB＝4，AC＝6，则AD的取值范围是（ ）
A、AD＞1 B、AD＜5 C、1＜AD＜5 D、2＜AD＜10
16、下列命题错误的是（ ）
A、两条直角边对应相等的两个直角三角形全等；
B、一条边和一个锐角对应相等的两个直角三角形全等
C、有两边和其中一边的对角（此角为钝角）对应相等的两个三角形全等
D、有两条边对应相等的两个直角三角形全等
17、如图8、△ABC中，AB＝AC，BD⊥AC于D，CD⊥AB于E，BD和CE交于点O，AO的延长线交BC于F，则图中全等直角三角形的对数为（ ）
A、3对 B、4对 C、5对 D、6对
 |
三、解答题与证明题：
18、如图，已知AB∥DC，且AB＝CD，BF＝DE，
求证：AE∥CF，AF∥CE
 |
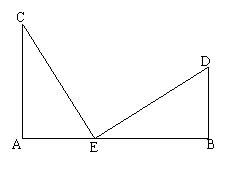19、如图，已知AC⊥AB，DB⊥AB，AC＝BE，AE＝BD，试猜想线段CE与DE的大小与位置关系，并证明你的结论。
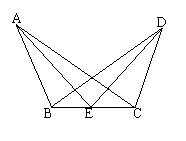
20、如图，已知AB＝DC，AC＝DB，BE＝CE
求证：AE＝DE
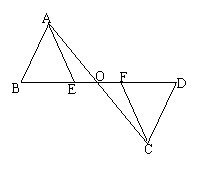
21、已知如图，E、F在BD上，且AB＝CD，BF＝DE，AE＝CF
求证：AC与BD互相平分
 |
22、如图，∠ABC＝90°，AB＝BC，D为AC上一点，分别过A、C作BD的垂线，垂足分别为E、F
求证：EF＝CF－AE
 |
参考答案：
1、DF，EF，DE；2、△ACD，等腰；3、∠B＝∠DEC，AB∥DE；4、三，△ABE≌△CDF，△ADE≌△CBF，△ABD≌△CDB；5、4；6、90°；7、108°；8、10cm；9、AAS，对应边上的高；10、135°。
11、B；12、D；13、A；14、D；15、C；16、D；17、D；
18、∵AB∥DC ∴∠ABE＝∠CDF，又DE＝BF，∴DE＋EF＝BF＋EF，即BE＝DF；
又AB＝CD，∴△ABE≌△CDF，∴AE＝CF，∠AEB＝∠CFD，
∴AE∥CF，再通过证△AEF≌△CFE
得∠AFE＝∠CEF，∴AF∥CE
19、猜想：CE＝ED，CE⊥ED，先证△ACE≌△BED
得CE＝ED，∠C＝∠DEB，而∠C＋∠AEC＝90°
∴∠AEC＋∠DEB＝90°
即CE⊥ED
20、先证△ABC≌△DCB
得∠ABC＝∠DCB
再证△ABE≌△DCE，得AE＝DE
21、由BF＝DF，得BE＝DF
∴△ABE≌△CDF，∴∠B＝∠D
再证△AOB≌△COD，得OA＝OC，OB＝OD
即AC、BD互相平分
22、证△ABE≌△BCF，得BE＝CF，AE＝BF，
∴EF＝BE－BF＝CF－AE