初二第二学期月考数学试卷

第二学期月考数学试卷

1.仔细选一选（每题3分，共30分）

(1)如果一个多边形的内角和等于一个三角形的外角和，那么这个多边形是(　　)

A.三角形　　  　B.四边形　　  　C.五边形　　  　D.六边形

(2)一组对边平行，另一组对边相等的四边形是(　　)

A.平行四边形　 B.梯形　　　 　 C.等腰梯形　　　D.平行四边形或梯形

(3)在平行四边形、矩形、菱形、正方形、等腰梯形中，对角线相等的图形有(　　)

A.2个　　　　　 B.3个　　　　 　C.4个　　　　　 D.5个

(4)平行四边形的对角线和它的边组成的全等三角形有(　　)

A.2对　　　　　 B.6对　　　　　 C.4对　　　　　 D.8对

(5)平行四边形周长是60cm,那么较长的对角线至多不超过(　　)

A.20cm　　　　　B.30cm　　　 　 C.40cm　　　　　D.60cm

(6)已知△ABC，若存在点D使以A、B、C、D为顶点的四边形是平行四边形，则这样的点D有(　　)

A.1个　　　　　 B.2个　　 　　　C.3个　　　 　　D.4个

(7)任意三角形两边中点连线与第三边的中线(　　)

A.互相平分　　　B.互相垂直　 　 C.相等　　　 　 D.互相垂直且平分

(8)菱形的周长为12cm,较长的对角线所对的角为120°，那么较短的对角线长为(　　)

A.4.5cm　　　　 B.4cm　　　　　 C.3.5cm　　　　 D.3cm

(9)梯形中位线长为12，上、下底的比为1∶3，那么这梯形上下底的长为(　　)

A.6，18　　  　 B.3，9　　　 　 C.4，12　　　　 D.5，20

(10)在矩形、菱形、平行四边形、等腰梯形中，四边中点的线段组成的四边形为菱形的有(　　)

A.1个　　  　　 B.2个　　　　　 C.3个　　　　 　D.4个

2.认真填一填（每题3分，共30分）

(1)一个多边形的每一个内角都等于108°，则它的内角和是________

(2)在线段、角、等腰三角形、平行四边形、梯形、矩形、菱形、正方形这些图形中，轴对称图形是________，中心对称图形是_________

(3)等腰三角形的一腰长为5，在它的底边上任取一点作两腰的平行线，则所得平行四边形周长是_______

(4)在梯形ABCD中，AD∥BC，∠B=90°,∠C=30°，若AB=8cm,则DC长是________

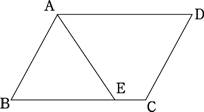
(5)如图，AE是平行四边形ABCD中∠A的平分线，CD=5cm，那么BE=________

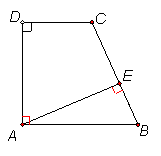
(6)如图，在梯形ABCD中，AB∥CD，∠D=90°，AE⊥BC，AB=BC=a,若CE=BC,则CD=________AB

(7)已知等腰梯形的一腰长2cm，一底边长为5cm，一钝角为120°，则其周长为________

(8)已知：两边都互相垂直的两角之差是40°，则这两个角分别等于________度和________度.

(9)一个四边形既是矩形又是菱形，它一定是________.

(10)等腰梯形ABCD中，AB∥CD，中位线长为8cm，且AB∶CD=3∶5，则AB=________,CD=________

3.请你答一答（每题10分，共40分）

(1)如图，已知梯形ABCD的中位线EF=16cm,它的一条对角线分中位线成两部分的差为4cm，求梯形两底AD和BC的长.

　　　　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　

 (2)已知等腰梯形两底和为11，腰长为3，锐角为60°，求作此梯形(不写作法，只保留作图痕迹).

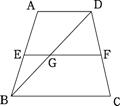
(3)如图，在梯形ABCD中，AD∥BC，E、F分别为BD和AC中点，BD平分∠ABC，求证：①AE⊥BD  ②EF=(BC-AB).

　　　　  　　　　　　　　　　　　 

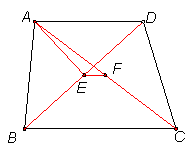
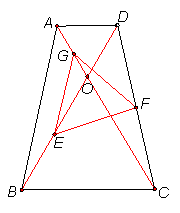
(4)如下图，AB∥CD，AD=BC,∠AOB=60°，E、F、G分别是OD、BC、OA中点，求证：△EFG为等边三角形.

　　　　　　　　　　　　　　　　　　　　　　　　 

比一比赛一赛，看谁能力强！

1.梯形ABCD中，AD∥BC，M、N分别是AD、BC的中点，若∠B与∠C互余，则2MN与BC-AD的关系是(　　)

A.2MN＜BC-AD　　　 B.2MN＝BC-AD　　　 　 C.2MN＞BC-AD　　　 D.无法确定

2.梯形的上底为a，下底为b，则梯形被其中位线分成的两部分面积之比为(　　)

A.　　　　 　 B.　　  C.　　　 D.

3.一梯形的中位线将梯形的面积分成1∶2，则上底a，中位线b，下底c之比为(　　)

A.1∶2∶3　　　 B.1∶2∶5　　　 C.3∶4∶5　　 　D.1∶3∶5

4.已知矩形的周长为p，对角线长为d，那么矩形的长与宽之差为(　　)

A.　　B. 　C.　　D.

5.等腰梯形两底为4cm，10cm，面积为21cm²，则较小的底角是(　　)

A.30°　　　　　B.45°　　　　　C.60°　　　　　D.90°

6.正方形ABCD的边长为1，E是AC上一点，且AE＝1，EF⊥AC交BC于F，则下列结论成立的是(　　)

A.BF＝ 　B.BＦ＝-1　 C.BF＝　　　　D.BF＝(2-1)

7.等腰梯形的两条对角线互相垂直，那么梯形的高h和中位线长m的大小关系是(　  )

A.m＞h　　　　　B.m＜h　　　　 C.m＝h　　　　　D.不能确定

8.在梯形ABCD中，已知AB∥CD，E是BC的中点，设△EDA的面积为S₁，梯形的面积为S₂，则S₁与S₂的关系是(　　)

A.S₁＝S₂　　　 B.S₁＝S₂　　 　C.S₁＝S₂　　　 D.S₁＝S₂

9.在菱形ABCD中，AE⊥BC于点E，AF⊥CD于点F，且E、F分别为BC、CD的中点，则∠EAF等于(　　)

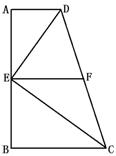A.75°　　  　　B.60°　　　　 C.45°　　　　　D.30°

10.如图，直角梯形ABCD中，AD∥BC，∠B＝90°，EF是

中位线，ED、EC分别平分∠ADC和∠BCD.下面的结论：

①　　　  △DEC是直角三角形；②AD+BC＝DC；③点E到DC的距离

等于AB；④DE·EC＝EF·AB，其中正确结论的个数是(　　)