初二数学期中模拟卷
班级 学号 姓名 成绩________
一、填空(每小题2分，共30分)
1、
的平方根是 ， 64的立方根是＿＿＿＿＿
2、 已知：
，则x＝ ；当x 时，
有意义。
3、 计算：
＝
。
4、 一个多边形的内角和等于1080°，则它是＿＿＿边形。
5、已知直角梯形的一腰长10 cm，这条腰和底边所成的角是300，另一腰是 cm，如果上底为3 cm，则这个直角梯形的面积是 cm 2。
6、如图（2），平行四边形ABCD的周长40cm，对角线AC、BD交于点O，若△ABO的周长比△BOC的周长小6cm则AD＝＿＿＿＿＿DC＝＿＿＿＿
7、如图（3），平行四边形ABCD中，∠B＝60°，AE⊥BC，AB＝2，BC＝4，则平行四边形ABCD的面积＝＿＿＿＿＿＿，AB、CD间的距离＝＿＿＿
 |  | ||
8、如果菱形的周长为16．8cm，相邻两角的度数之比为5：1，那么这个菱形的一组对边的距离是 。
9、当
时，
。
10、已知a为
的整数部分，b为的小数部分，
则
＝ 。
二、选择题（每题3分，共24分）
1、在下列实数
，3.，
，－8，
中无理数有（ ）
A 、3个 B、 4个 C、 5个 D、6个
2、下列命题正确的是（ ）
A、一组对边平行，另一组对边相等的四边形是平行四边形。
B、对角线相等的四边形是平行四边形。
C、一组对边平行，一组对角相等的四边形是平行四边形。
D、以上命题都不对。
3、下列命题中不正确的是（ ）
A、整数和有限小数统称为有理数 B、无理数都是无限小数
C、数轴上的点表示的数都是实数 D、实数包括正实数、负实数和零
4、在根式
中，最简根式有（ ）
A、2个 B、3个 C、4个 D、5个
5、
，那么a与b的关系是（
）
A、互为相反数 B、互为倒数 C、相等 D、以上都不是
6、把式子
根号外的因式移入根号内得（ ）
A、
B、
C、
D、
7、四边形的四条边依次为a、b、c、d，满足a2＋b2＋c2＋d2＝ab＋bc＋cd＋ad，则四边形是( )
A．平行四边形 B．矩形 C．菱形 D．正方形
8、在下列图形中，是中心对称图形而不是轴对称图形的是( )
A．正方形 B．角 C．射线 D．平行四边形
三、计算或化简（每题4分，共20分）
1、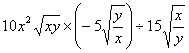
2、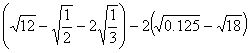
3、
4、当
时，化简
5、已知，直角三角形的两条直角边a＝
＋1，b＝
，求斜边c及直角三角形的面积。
四、作图题：（5分）
1、画梯形ABCD，使底AD＝a BC＝ b，腰AB＝c，∠B＝600。（不写画法，保留作图痕迹）
五、解答题
1、等腰梯形ABCD中，AB＝2CD，AC平分∠DAB，AB＝4，AB∥CD，
(1) 求此梯形各角；(2) 求梯形面积．(5分)
2、如图，以Rt△ABC的直角边AC、BC向形外作正方形ACGH、正方形CBEF，连结GE、AE．
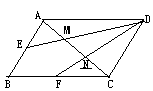求证：(1)AE＝GE；(2)EC垂直平分AG．
3、已知：如图：△ABC中，AM＝MN＝NC，E、F为AB、BC中点，EM，FN的延长线交于D，
求证：四边形ABCD是平行四边形。(5分)
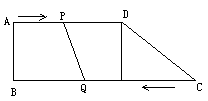
4、如图所示，在直角梯形ABCD中，AD//BC，∠B＝900， AD＝24 cm，AB＝8 cm，BC＝26 cm，动点P从A开始沿AD边向D以1 cm/S的速度运动，动点Q从点C开始沿CB边向B以3 cm/S的速度运动，P，Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒，t分别为何值时，四边形PQCD为平行四边形，等腰梯形？(6分)
《参考答案》
一、1、±3 ；4 2、4或－2； 3、1．5 4、10； 5、5；
6、13；7； 7、
8、2．1； 9、2
10、
二、1、A 2、C 3、A 4、B 5、A 6、B 7、C 8、D
三、1、
2、
3、
4、6－3x
5、
四、略
五、1、(1)∠DAB＝∠B＝600，∠ADC＝∠DCB＝1200； (2)S＝
2、(1)证：连结CE
∵四边形ACGH、CBEF是正方形
∴AC＝CG，∠CFE＝∠BCF＝450
∵∠ACB＝∠QCF＝900
∴∠ACE＝∠GCE
∵CE＝CE
∴△ACE≌△GCE
∴AE＝GE
(2)∵AC＝CG，AE＝GE
∴C、E都在线段AG的中垂线上
∴CE垂直平分AG
2、证明：连结BM、BN、BD，BD与AC相交于O
∵AM＝MN，AE＝EB
∴EM∥BN，即MD∥BN
同理BM∥ND
∵四边形BMDN是平行四边形
∴MO＝ON，BO＝OD
∵AM＝NC
∴AO＝OC
∴四边形ABCD是平行四边形。
4、(1)要使PQCD为平行四边形，则PD∥CQ且PD＝CQ
∴ 24－t＝3t
t＝6
∴当t＝6时四边形PQCD为平行四边形
(2) 作DE⊥BC，
AB＝BE＝8cm，AD－＝BE＝24cm
∴EC＝BC－BE＝26－24＝2cm
要使PQCD为等腰梯形，则CQ＝DP＋2CE
∴3t＝(24－t)＋4
t＝7
∴当t＝7秒时，四边形PQCD为等腰梯形。