初中数学夏令营赛前专题训练(九)
代 数 (B)
1. 解方程组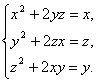
2. 设a , b ,p , q
, r , s为正整数,满足qr-ps=1, 
＜
＜
。证明：b≥q+s。
3. 求证:不存在这样的整数,把它的首位数字移到末位之后,得到的数是原数的两倍.
4. 一个四边形在边长为1的正方形各边上各有一点,证明四边形的边长a,b,c,d满足不等式2≤a
+b+c
+d≤4.
5. 观察
=
+；=
+
；=
+
；=
+
。由这些例子的启发，叙述一般规律，并加以证明。对任何大于1的整数n，证明存在正整数i和j，使得
6. 汽车路线由周长10英里的环路和从总站到环路上Q点长1英里的直线组成（如图），两部汽车在路上服务，每部周游需要20分，1号车离开总站，沿着直路走，按顺时针方向绕环路一次，又沿直线回到总站，2号车到达总站比1号车迟到10分，走同样的路线，但按返时针方向绕行环路。两部车连续行驶，在路上的任何地点都不耽搁，只有让乘客上、下车的时间可以忽略。
一个人打算在地点P候车，那里沿1号车路线离开总站x英里（0≤x＜12＝要搭车到总站去,假定他搭上使他尽早达到目的地的汽车,他的旅行所需的最长的时间为W(x) (候车时间加乘车时间).
求W(2),W(4).
对于x的什么值, 时间W(x)最长?
对0≤x＜12画出y = W(x)的草图.