初中数学夏令营赛前专题训练（六）
代数（A）
1、实数x与y，使得x+y， x－y，xy，
四个数中三个有相同的数值，求出所有具有这样的数对（x，y）
2、如果a为不等于±2的整数，证明方程x4+ax+1 = 0没有有理根。
3、已知a，b，c，d是两两不等的正整数，并且
a+b= cd
ab = c+d
求出所有满足上述要求的四元数组（a，b，c，d）
4、求方程7（x+y）=3（x2－xy+y2）的整数解。
5、若四个非零的实数a，b，c，d适全下列条件：
（1）a2+b2+c2+d2=1
（2）a2+b2+c2+d2 = a+b+c+d
（3）a（
+
+
）+b（++
）+c（++）+d（++）=－4
试证：a+b+c+d为定值，
6、设a为给定的正整数，A和B为实数，又给出下面的方程组，
=
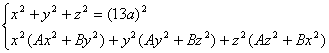
(2A＋B)(13a)4
证明：（1）当A= 
B时，方程组有正整数解，
（2）当A≠ B时，方程组没有正整数解。