第二届澳门中学生数学冬令营试题

第二届澳门中学生数学冬令营　 第一轮选拔赛

比赛日期：2002年1月5日，答题时间：三小时半。
请回答题目1至4，每题同分。不能使用任何计算器。

1. 设a、b为整数使得存在连续整数c、d满足a-b=a²c-b²d。求证：a-b是完全平方数。
   　
2. 试求所有可能的正整数n，使得一块9 x n的长方形木板能够用若干以下的图形(见下图)所覆盖，而且任何两个互不重迭。每个图形由三个1 x 1的磁砖所成，必要时可旋转。请证明你的答案。
   
3. 设O为三角形ABC的旁切圆的圆心，且圆O分别与线段BC、AB的延长线、AC的延长线相切于点K、P、Q。设M为直线OB、PQ的交点，N为直线OC、PQ的交点。求证：

QN AB

=

MN BC

=

MP CA

。

4. 设a、b为正实数，求证：。

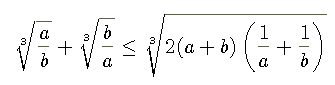First Round of the 2nd Macau Mathematical Olympiad Winter Camp
Date: 5th Jan, 2002.　Time allocated: 3 hours and 30 minutes.
Answer all 4 questions.Electronic calculator is not allowed.

1. Let a and b be integers. Suppose that there exist consecutive integers c and d such that a-b=a²c-b²d. Prove that a-b is a prefect square.
   　
2. Find all possible values of n such that a rectangular board 9 x n can be covered by a number of the following shapes (illustrated below) without overlapping. Each of these shapes is formed by 3 tiles of dimensions 1x1, and it can be rotated if necessary.Give a proof of your answers.
   
3. Given a triangle ABC, let O be the centre of the excircle of ABC which touches side BC, extended line AB and extended line AC at points K, P and Q respectively. Let M be the intersection of OB and PQ, and N be the intersection point of OC and PQ. Prove that

QN AB

=

MN BC

=

MP CA

.

4. Let a and b be two positive numbers, prove that
   .

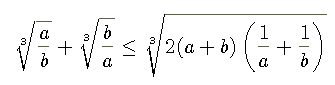 第二届澳门中学生数学冬令营
第二轮选拔赛

比赛日期：2002年1月6日
答题时间：三小时半
请回答题目1至4，每题同分。不能使用任何计算器。

1. 设正方形ABCD的对角线相交于点S，设P为边AB的中点。设M为线段AC与PD的交点，N为线段BD与PC的交点。已知一个圆O内切四边形PMSN。求证：圆O的半径为MP－MS。
   　
2. 设集合S有100个正整数，每个整数小于200。求证：存在S的一个非空子集T使得T的所有元素之积是个完全平方数。
   　
3. 有一个n x n的方格表，每个格填入数字0或1的其中一个，不能重复。已知任意两行和任意两列相交的四个方格至少包含一个0，求证：在表格内1的总数不大于。
   　
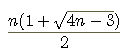4. 设a、b、c为非负实数，求证以下不等式成立：
   
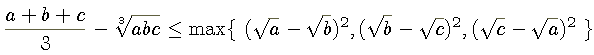
   其符号 max{A, B, C} 代表实数A、B、C的最大值。

Second Round of the 2nd Macau Mathematical Olympiad Winter Camp

Date: 6th Jan, 2002.　Time allocated: 3 hours and 30 minutes.
Answer all 4 questions.Electronic calculator is not allowed.

1. Let S be the intersection of the diagonals of a square ABCD, Let P be the midpoint of AB. Let M be the intersection of AC and PD, and N be the intersection of BD and PC. A circle O is inscribed in the quadrilaterial PMSN. Prove that the radius of the cricle O is equal to MP-MS.
   　
2. Let S be a set of 100 positive integers, each of them is less than 200. Prove that there exists a nonempty subset T of S such that the product of all its elements is a perfect square.
   　
3. There is a n x n table filled with 1's and 0's. Suppose that four squares on the intersections of any 2 rows and two columns contain at least one 0. Prove that the number of 1's is not greater than .
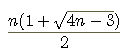4. Let a, b and c be non-negative real numbers, prove the following inequality:
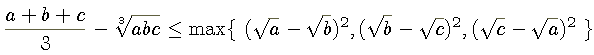
   where max{A, B, C} is the maximum of real numbers A, B and C.