我爱数学初中生夏令营数学竞赛试卷

　　　　　 2001我爱数学初中生夏令营数学竞赛试卷（第一试）

一．在锐角ΔABC中，AD⊥BC，D为垂足，DE⊥AC，E为垂足。O为ΔABC的外心。

求证：（1）ΔAEF～ΔABC；（2）AO⊥EF。

二．给定代数式 –x³+100x²+x 中的字母 x只允许在正整数范围内取值。当这个代数式的值达到最大值时， x的值等于多少？并证明你的结论。

三．（1）证明存在非零整数对（x,y）, 使代数式 11x²+5xy+37y² 的值为完全平方数；

(2) 证明存在六个非零整数a₁,b₁,c₁,a₂,b₂,c₂, 其中a₁:a₂≠b₁:b₂,使得对于任意自然数n, 当x=a₁n²+b₁n+c₁,y=a₂n²+b₂n+c₂ 时，代数式 11x²+5xy+37y²的值都是完全平方数。

2001我爱数学初中生夏令营数学竞赛试卷（第二试）

一． =　　　　。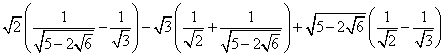

二．在长方形ABCD中，EF∥AB，GH∥AD，EF与GH相交于O，

HC与EF相交于I。已知AH:HB=m:n, △COI的面积为1平方厘米，

那么矩形ABCD的面积等于　　　　  平方厘米。

三．将三个数： 用两个不等号“>”连接起来，正确的结果应该是：　　　　。

四．点D，E分别在△ABC的边AC和BC上，∠C为直角，DE∥AB，

且3DE=2AB，AE=13，BD=9，那么AB的长等于　　　　 。

五．知：x,y,z是正整数，并且满足

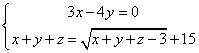
那么，x-y+z 的值等于　　　　。

六．已知点D，E，F分别在△ABC的三边BC，CA，AB上，G为BE与CF的交点，并且BD=DC=CA=AF，AE=EC=BF，那么的值等于　　　　。

七．如果满足 x²-6x-16-10 = a的实数x 恰有6个，那么实数a的值等于　　　　。

八．已知△ABC为等腰直角三角形，∠C为直角，延长CA至D，以AD为直径作圆，连BD与圆O交于点E，连CE，CE的延长线交圆O于另一点F，那么的值等于　　　　。

九．满足下列两个条件

（1）对所有的自然数，x，x-2001x+n≥0;

（2）存在自然数x₀，使x₀²-2002 x₀+n<0.

的正整数n的个数为

十．一批救灾物资分别随16列货车从甲站紧急调运到三百多里以外的乙站，已知每列货车的平均速度都相等，且记为v公里/小时。两列货车实在运行中的间隔不小于公里，这这批救灾物资全部运到目的地最快需要6小时，那么每隔　　　　分钟从甲站向乙站发一

趟货车才能使这批货物在6小时内运到。