第一届澳门中学生数学冬令营试题

第一届澳门中学生数学冬令营
第一轮选拔赛

比赛日期：2000年12月16日
答题时间：三小时
请回答题目1至4，每题同分
不能使用任何计算器
　

1. 两个圆C₁、C₂相交点M、N，点P、Q分别在圆C₁、C₂上使得
   直线PQ为圆C₁、C₂的(较近于N)一条公共切线。证明：三角形MNP、MNQ有相同的面积。
   　
2. 已知x、y、z为正实数且xyz=32。试求x²+4xy+4y²+2z²的极小值。
   　
3. 试求正整数a、b使得。
   　
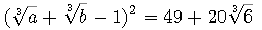4. (a)试找出一个有10个两两不同的正整数集合A，使得A的任意6个不同的元素之和不是6的倍数。
   (b)若将集合元素数目从‘10’改为‘11’，问能否找到集合A具有相同的性质？

第一届澳门中学生数学冬令营
第二轮选拔赛

比赛日期：2000年12月17日
答题时间：三小时
请回答题目1至3，每题同分
不能使用任何计算器

1. 设n≧3为自然数，证明下述的论断只对n=3和n=5成立：
   对于任意的实数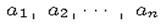，有
   
   。
   　
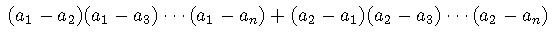
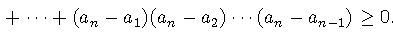2. 对每个自然数n，求最大的整数k，使得可在任意一个n个元素的集合A取出A的k个子集，其中任意两个子集的交集非空。
   　
3. 在一个已知锐角三角形的三边上各找一点，使这三点作顶点的三角形周长最小。