富春三中八年级数学整式的乘法B
一、精心选一选(每题2分,共20分)
1、下列运算中正确的是( )
A、(x+3y)(x-3y)=x2-3y2 B、(x-3y)(x-3y)=x2-9y2
C、(-x+3y)(x-3y)=-x2-9y2 D、(-x-3y)(-x+3y)=x2-9y2
2、在下列各式中计算正确的是( )
A、(5a+3b)2=25a2+9b2 B、(7x-2y)2=49x2-14xy+4y2
C、(4y-3)2=16y2+24y+9 D、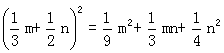
3、下列计算结果为2xy-x2-y2的是( )
A、(x-y)2 B、(-x-y)2 C、-(x+y)2 D、-(x-y)2
4、下列各式中是完全平方展开式的是( )
A、4x2+4x-1 B、1-4x-4x2 C、-4x+4x2+1 D、4x2-2x+1
5、下列各式从左到右的变形属于因式分解的是( )
A、(m-2)(m-1)=(2-m)(1-m) B、1-a2=(1-a)(1+a)
C、(2x+1)(x-2)=2x2-3x-2 D、4a2+4ab+b2=4a(a+b)+b2
6、下列各式中,能用平方差公式a2-b2=(a+b)(a-b)分解因式的是( )
A、x2+y2 B、xy2-m2 C、-a2-b2 D、-1+x2
7、(-x-y)2展开后的结果是( )
A、-x-2xy-y2 B、x2+2xy+y2
C、-x2-2xy+y2 D、x2-2xy+y2
8、若(3x+2y)2=(3x-2y)2+A,则代数式A为( )
A、-12xy B、12xy C、24xy D、-24xy
9、三个连续偶数,中间一个是k,则它们的积为( )
A、k3-k B、k3-4k C、4k3-k D、8k3-2k
10、如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形,通过计算两图形(阴影部分)的面积,验证了一个等式,此等式是( )
A、(a+b)2=a2+2ab+b2 B、(a-b)2=a2-2ab+b2
C、a2-b2=(a+b)(a-b) D、(a+2b)(a-b)=a2+ab-b2
二、细心填一填(每题2分,共16分)
11、(3x+5y)(3x-5y)=( )2-( )2=__________。
(2x-y)2=( )2-2·_____·_____+( )2=___________。
12、(-m-n)(-m+n)=_________,(2m+3)(3-2m)=_____________。
13、(-2x+3y)2=___________, 9x2-________+16y2=(3x-____)2
14、x2+10x+_____=( )2, 4m2-12mn+____=( )2
15、3x3+6x2=______(x+2),x2y+xy2-xy=xy( ).
16、分解因式:9x2-4y2=( )2-( )2=____________;
9x2-12xy+4y2=( )2+( )2-2·_____·_____=__________;
17、若m2-n2=15,m+n=5,则m-n=_________。
18、若(x+y)2=36,(x-y)2=4,则x2+y2=_______,xy=______.
三、考考你的基本功(第19题18分,第20题24分,共42分)
19、计算下列各题,能用乘法公式的尽量利用乘法公式:
(1)(-m-n)(n-m) (2)(-m+n)(m-n)
(3)(2x+6)2-2(3-x)2 (4)[(a+2b)-c]2
(5)(2a+b+1)(2a-b+1) (6)(m+3)(m-3)(m2-9)
20、把下列各式因式分解:
(1)3a2y-3ay2+6y (2)x5-x3
(3)![]() (4)-12xy-9x2-4y2
(4)-12xy-9x2-4y2
(5)2pm2-12pmn+18pn2 (6)(a+b)2-4(a+b)+4
(7)m4-n4 (8)(x-1)(x-3)+1
四、努力用一用(第21、24每题6分,第22、23题每题5分,共22分)
21、用简便方法计算:
⑴20042-2005×2003 ⑵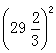
22、已知a-b=3,ab=10,求a2+b2的值。
23、试说明两个连续奇数的平方差必是8的倍数。
24、教你一招:把a2-2ab+b2-c2因式分解。
解:原式=(a2-2ab+b2)-c2
=(a-b)2-c2
=(a-b+c)(a-b-c)
请你仔细阅读上述解法后,把下列多项式因式分解:
⑴4x2-4xy+y2-a2
⑵1-m2-n2+2mn