2005年12月八年级上数学月考复习（一）
一、选择题：（每题3分，共３0分）
1、已知点P1(-4，3)和P2(-4，-3)，则P1和P2( )
A、关于原点对称 B、关于y轴对称 C、关于x轴对称 D、不存在对称关系
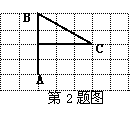2、如图是在方格纸上画出的小旗图案，若用(0，0)表示A点，(0，4)表示B点，那么C点的位置可表示为( )
A、(0，3) B、(2，3) C、(3，2) D、(3，0)
3、如果P（m+3,m+1）在直角坐标系的x轴上，则点P坐标为（ ）
A、（0，2） B、（2，0） C、（4，0） D、（0，-4）
4、一元一次不等式组
的解集为x>a，且a≠－1，则a取值范围是（ ）。
A、a>－1 B、a<－1 C、a>0 D、a<0
5、－
的值是非负数，则x的取值范围是（ ）。
A、x≤－1 B、x≥－1 C、x≥1 D、x≤1
6．将△ABC的3个顶点坐标的纵坐标乘以－1，横坐标不变，则所得图形与原图形的关系是（ ）。
A．关于x轴对称 B．关于y轴对称
C．关于原点对称 D．将原图向x轴的负向平移了1个单位
7．将点M（a，b）向上平移3个单位，所得的像的坐标是（ ）。
A．（a－3， b） B．（a+3， b） C．（a，b－3） D．(a,b+3）
8、若y关于x的函数解析式为y=kx－9,当x=3时,函数值为6，则当x=－3时函数值为：（ ）
A、－6 B、－12 C、－24 D、－36
9、已知△ABC的面积为3，边BC长为2，以B原点，BC所在的直线为x轴，则点A的纵坐标为( )
A、3 B、-3 C、6 D、±3
10、在直角坐标系中，O为坐标原点，已知A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数共有 （ ）
A、4个 B、3个 C、2个 D、1个
二、填空题：（每题3分，共36分）
11、数据1，3，2，5，4的方差是 ，标准差是 。
12、为了预防“禽流感”的传播，检疫人员对某养殖场的家禽进行检验，任意抽取了其中的100只，此种方式属 调查，样本是 ，样本容量是 。
13、函数
中自变量x的取值范围是
。
| 平时 | 期中 | 期末 |
| 84 | 90 | 87 |
14. 小明在一个学期的数学测试成绩如下：
学期成绩按平时、期中、期末各占30%、30%和40%记，
小明的数学学期成绩是__ 分。
15、小明帮助父母预算11月份电费情况，下表是11月初连续8天每天早上电表的显示读数：
| 日 期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 电表显示读数 | 21 | 24 | 28 | 33 | 39 | 42 | 46 | 49 |
如果每度电费用是0.53元，估计小明家11月（30天）的电费是 元。
16、点A在x轴上方，距x轴4个单位长度，距y轴3个单位长度，则A点的坐标是____________，A点离开原点的距离是________ 。
17、不等式-4<1-3x≤4的整数解为__________。
18、已知
，若把y看成x的函数，则可表示为
。
19、已知线段MN平行于x轴，且MN的长度为5，若M（2，-2），那么线段MN上任意一点的坐标是__________.
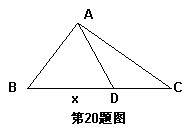
20、如右图，△ABC边BC长是10，BC边上的高是6cm,D点在BC上运动，设BD长为x,请写出△ABD的面积y与x之间的函数关系式： __________，自变量x的取值范围是________，函数值y的取值范围是___________。
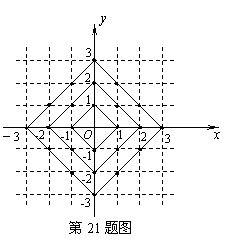
21、在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点. 观察图4中每一个正方形（实线）四条边上的整点的个数，请你猜测由里向外第10个正方形（实线）四条边上的整点个数共有_________个.
22、根据指令[s,A] (s≥0, 00<A<1800), 机器人在平面上能完成下列动作: 先原地逆时针旋转角度A, 再朝其面对的方向沿直线行走距离s. 现机器人在直角坐标系的坐标原点, 且面对x轴正方向. (1) 若给机器人下了一个指令[4,600]，则机器人应移动到点 ____; (2) 请你给机器人下一个指令 ____ , 使其移动到点 (-5,5).
三、解答题（共51分）
23、（8分）解下列不等式（组），并把解集表示在数轴上。
（1）
≥
（2）
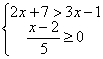
24、（8分）已知
与x成正比例，且
时，
。
（1）y是x的一次函数吗？求y与x之间的函数关系式；
（2）求当x=1时y的值；
（3）求当y=3时x的值；
（4）求当-1<y≤2时x的取值范围。
25、（8分）浙江省移动公司开设有两种手机业务：①“全球通”：月租费为50元，市内通话费按0.4元/分计算；②“神州行”：不缴月租费，市内通话费按0.6元/分计算.若设一个月市内通话时间为x分，两种方式的通话费分别为和.则选择全球通合还是神州行合算？
26、（8分）一次科技知识竞赛，两组同学成绩统计如下表：
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
| 乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
请你根据所学过的统计知识，判断这次竞赛中成绩谁优谁劣，并说明理由。
27、（9分）某小区按照分期付款的形式福利购房，政府给予一定的补贴。小明家购得一套现价为120000元的房子，购房时首期（第一年）付款30000元。从第二年起，以后每年付房款为5000元与上一年剩余欠款利息的和，设剩余欠款的年利率为0.4％。
（1）若第x（
）年小明家交付房款y元，求年付款y（元）与x（年）的函数关系式；
（2）将第三年、第十年应付房款填入下列表格中。
| 年份 | 第一年 | 第二年 | 第三年 | …… | 第十年 |
| 交房款（元） | 30000 | 5360 | …… |
28、（10分）如图，公路上有A、B、C三站，一辆汽车在上午8时从离A站10 km的P地出发向C站匀速前进，15 min后离A站 20 km。
（1）设出发x h后，汽车离A站y km，写出y与x之间的函数关系式；
（2）当汽车行驶到离A站150 km的B站时，接到通知要在中午12时前赶到离B站30 km的C站。汽车若按原速度能否准时到达？若能，时几时几分到达？若不能，车速最少应提高到多少？