初二数学竞赛练习题
一、选择题
1．已知实数
、
满足：
且
，
，则
、
的关系
为（C）
A．
B．
C．
D．M、N的大小不能确定
2．关于
的不等式
的解是
，则不等式
的解为（A）
A．
B．
C．
D．
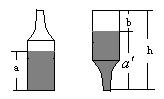4．如图，啤酒瓶高为
，瓶内酒面高为，若将瓶盖好
后倒置，酒面高为
（
），则酒瓶的容积与
瓶内酒的体积之比为（C）
A．
B．
C．
D．
5．正三角形ABC所在平面内有一点P，使得△PAB、△PBC、△PCA都是等腰三角形，则这样的
P点有（D）
A．1个 B．4个 C．7个 D．10个
二、填空题
6．方程
的解是 x=11 ；
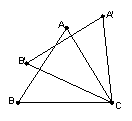
7．如图，把ΔABC绕点C顺时针旋转
，得到⊿
，
交AC于D，已知∠
＝
，则∠A的度数是 65˚ ；
8．已知
，则
＝ 2006 ；
9．已知直角梯形ABCD中，AD∥BC，AB＝BC，∠A＝，∠D＝
，CD的垂直平分线交CD于E，交BA于的延长线于F，若AD＝9
，则BF＝ 9 ；
10．已知四边形的四个顶点为A（8,8），B（－4,3），C（－2，－5），D（10，－2），则四边形在第一象限内的部分的面积是
。
11．如图，长方形纸片ABCD中，AB＝3，BC＝4，
现将A、C重合，使纸片折叠压平，设折痕为EF，则
图形中重叠部分△AEF的面积为
；
|
=
；
13．将
分解因式得
|
；
14．甲、乙两人在环形跑道上练习长跑，甲的速度与乙的速度的比为5∶3，若两人同时从同一点出发，则乙跑了 6 圈后，甲比乙多跑了4圈。
15．教室里共有8个人，每个人都和其余的每个人握一次手且只握一次手，则共握了 28次手．
16．已知△ABC为等腰三角形，由A点所引BC边的高线恰好等于BC边长的一半，
则∠BAC的度数为______________.
17．计算
－12 .
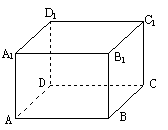
18．.如图，一个长方体盒子，一只蚂蚁由A出发，在盒子的表面上爬到点C1，已知AB=7cm，BC=CC1=5
cm ，则这只蚂蚁爬行的最短路程是
cm.
三、解答题：
19．甲、乙、丙、丁四人参加一次数学竞赛.赛后,他们四个人预测名次的谈话如下:
甲:“丙第一名，我第三名.”
乙：“我第一名，丁第四名.”
丙：“丁第二名，我第三名.”
丁没说话.
最后公布结果时,发现他们预测都只对了一半.说出这次竞赛的甲、乙、丙、丁四人的名次.
甲是第 3 名,乙是第 1 名,丙是第 4 名,丁是第 2 名.
20．已知直角三角形ABC的周长为20，面积为10，求它三边的长。
9,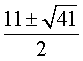 
21．已知三角形的一边是另一边的3倍，求证：三角形的最小边在周长的
与
之间。
证明:设三角形一边为，另一边为
，第三边的长为
则第三边满足：
………………………………………………3分
所以边长为的边为最小边
于是有 
……………………………………………6分
即
且
即
＜
所以最小边在周长的与之间。 …………………………………………10分
22．当等腰三角形被一条直线分割成两个较小的三角形也是等腰三角形时，原等腰三角形的顶角度数是多少？这条直线怎样画？（讨论所有可能的解，并逐一画图表示）
分两种情况讨论：
1、当直线通过等腰三角形的顶点时，有如左图的两个解：
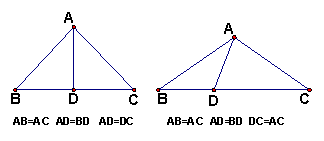顶角：、
2、当直线通过等腰三角形的底角顶点时，有如右图的两个解。
 |
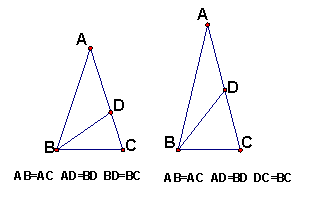顶角：
、
23．两辆汽车从同一地点同时出发，沿同一方向同速直线行驶，每车最多只能带24桶汽油，途中不能用别的油，每桶油可使一辆汽车前进60千米，两车都必须返回出发地点，但是可以不同时返回，也可以两车相互借用对方的汽油，为了使其中一辆车尽可能地远离出发点，另一辆车应当在离出发点多少千米的地方返回？离出发点远的那辆车一共行驶了多少千米？
解：设两辆汽车分别为甲、乙，并且甲用了桶汽油时返回，留下返程需要的桶汽油，将多余的（24－
）桶汽油给乙，让乙继续前进，………………………………2分
这时乙有：
桶汽油，
由题设：
≤24 得：≥8 ……………………………………5分
甲、乙分手后，乙继续前进的路程是
千米
这说明当值越小时，代数式的值越大，………………………………………8分
所以当
时，得最大值480千米
因此，乙行驶的路程是2（60×8+480）=1920千米。…………………………10分