第十一章 一次函数（B）
一.
知识技能:
1． 骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，
在这一问题中，自变量是（ ）
A．沙漠 B.体温 C.时间 D.骆驼
2.已知函数: ①y=-x-2;②y=
; ③y=-
x; ④y=
; ⑤2x+3y=6,其中不是一次函数的是( )
A. ①③ B. ③④ C. ②④ D. ③⑤
3.下面的直线中,经过点(0,-2)且与直线y=3x平行的直线是( )
A.y=3x+2 B.y=-3x+2 C.y=3x-2 D.y= -3x-2
4.如果正比例函数y=-kx,y随x的增大而增大,则一次函数y=kx+1的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限
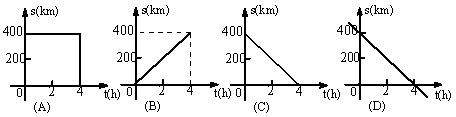
5.汽车由重庆驶往相距400km的成都,如果汽车的平均速度是100km/h,那么汽车距成都的路程s(km)与行驶时间t(h)的函数关系用图象表示应为如图中的( )
6.函数
的自变量x的取值范围是_____________________.
7.请写出同时具备下列两个条件的一次函数表达式(写出一个即可) __________________
(1)y随着x的增大而减少 (2)图象经过点(1,-2)
8.一种储蓄的月利率为0.27％,今存入本金200元,则本息和y(元)与所存月数x(月)之间的函数关系是________________.当存入1年后,本息和是____________元.
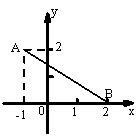
9.若函数的图象是线段AB(点A除外)如右图,
则此函数解析式为_______________________.
(要求写出自变量的取值范围)
.
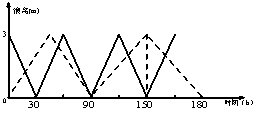10.一游泳池长90米,甲.乙二人分别在游泳池相对两边同时朝另一边游泳,图中的实线和虚线分别为甲.乙与游泳池一边的距离随游泳时间的变化而变化的图象,若不计转向时间,那么可以知道:
(1)甲游泳的平均速度是________________________;
(2)乙游泳的平均速度是________________________；
(3)从开始到3分他们相遇的次数为__________次.
11.已知s是t的一次函数,当t=8时,,s=15;当t=-10时s=3,求:
(1)这个一次函数关系式;
(2)当t= -14时,相应的s的值.
12.已知直线y1=2x+3与直线y2=-2x-1,利用图象回答下列问题:
(1)当x为何值时,y1=y2;
(2) 当x为何值时,y1>y2;
(3) 当x为何值时,y1<y2;
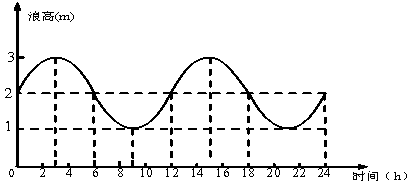
13.某城市的海滨浴场,波浪的浪高随时间变化的曲线如图所示:
(1)请问,这一天中,此浴场浪高的变化范围是什么?浪高最高到
最低要多少时间?
(2)在什么时间段中,浪高在增大?
(3)适合冲浪的浪高必须在2米以上.请问:在上午8时到下午18时,
哪一个时间段是适合冲浪的?
 |
14一种出租车的收费方式如下:4千米以内10元,4千米至15千米部分每千米加收1.2元,15千米以上部分每千米加收1.6元,某乘客要乘出租车去50千米处的某地.
(1)如果乘客中途不换车要付车费多少元?
(2)如果乘客中途换一辆出租车,他在何处换比较合算?
算出总费用与(1)比较
（二）能力活动
15.下列四个图象中,不表示某一函数图象的是( )
16.科学研究表明,当人的下肢长y(cm)与身高x(cm)的关系y=0.618x时,看起来最美,为此有的女士穿高跟鞋,使下肢显得更长点.某成年女士身高为153cm,下肢长92cm,该女士穿的高跟鞋鞋跟的最佳高度约为( )
A.2.6cm B.2.5cm C.6.7cm D.6.6cm
17.一次函数y=kx+b的自变量的取值范围是-3≤x≤6,相应函数值的取值范围是-5≤y≤-2,则这个函数解析式为________________________.
18.某工人上午7点上班至11点下班,他一开始用一定时间做准备工作,接着每隔相同时间加工1个零件,已知他加工完7个零件时刚好是9点,加工完11个零件时刚好是10点,则他做准备工作用了___________分钟.
19.已知函数y=(2m+1)x+m-3
(1)若函数图象经过原点,求m的值;
(2)若函数图象在y轴的截距为2,求m的值;
(3)若函数图象平行直线y=3x-3,求m的值;
(4)若这个函数是一次函数,且y随着x的增大而减少,求m的取值范围.
20.某辆摩托车油箱中原有汽油15L,摩托车每行45耗油1L.
(1)填写下表:
| 路程x(km) | 0 | 45 | 90 | 135 | 180 |
| 余油量y(L) |
(2)写出y与x的函数解析式;
(3)当行驶450km时,油箱中还有油多少L?
(4)如果加满油并且需要回来,最多能行驶多远?
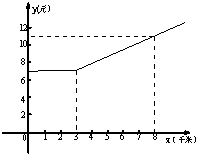
21.如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象.
(1)当行驶8千米时,应收费多少元?
(2)从图象上你能获得哪些信息?(请写出两条)______________,_________________
(3) 求出收费y(元)与行驶x(千米)之间的函数关系式.
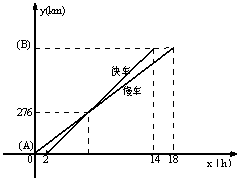
22.一慢车和一快车沿相同路线从A地到B地，所行的路程与时间的函数图象如图所示。根据图象，回答下列问题：
（1）慢车比快车早出发_________h,快车追上慢车时行驶了________km,快车比慢车早__________ h到达B地.
(2)在下列3个问题中任选一题求解:
①快车追上慢车需几个小时?
②求快车、慢车的速度.
③求A、B两地之间的路程.
23.甲.乙两个仓库要向A、B两地运水泥，已知甲库可调出100吨水泥，乙库可调出80吨水泥，A地需70吨水泥，B地需110吨水泥。两库到A，B两地的路程和运费如下表所示（元/t.km表示每吨水泥运一千米所需人民币）
| 路程（km） | 运费（元/t.km） | |||
| 甲库 | 乙库 | 甲库 | 乙库 | |
| A地 | 20 | 15 | 12 | 12 |
| B地 | 25 | 20 | 10 | 8 |
（1） 设甲库运往A地水泥x吨，求总运费y（元）关于x（吨）的函数关系式；
（2） 当甲、乙两库各运往A、B两地多少吨水泥时总运费最省，最省是多少？
一次函数(B)答案
一. 知识技能:
1.C 2.C 3.C 4.C 5.C 6.x≤3 7.y=-x-1 (答案不唯一) 8.y=0.54x+200 200.54 9. y=-2/3x+4/3(-1<x≤2) 10.3m/s 2m/s 5 11. ①s=2/3t+25/3 ②-1 12. ①x=-1 ②x>-1 ③x<-1 13. ① 1m～3m, 6h
②0时～3时, 9时～15时 , 21时～24时 ③12时～18时 14. ①79.2元 ②在离出发15千米处换车车费最少,最少费用为78.4元,比第一次乘省0.8元
二. 能力活动:
15.D 16.C 17.y=-1/3x-4或 y=-1/3+1 18 .15 19. ①m=3 ②m=5 ③m=1 ④m<-1/2 20. ①15,14,13,12,11 ②y=15-1/45x ③5 ④337.5km
21. ①11 ②略 ③y=1.2x+1.4 22. ①2, 276, 4 ②略 23. ①y=-94x+36640 (10≤x≤70) ②当x=70时,y最小值为30060元,此时甲库运往A地70吨,运往B地30吨,乙库运往A地0吨,乙库运往B地60吨.