第十一章 一次函数（A）
一．知识技能：
1，下列函数关系y中，变量y与x成正比例函数关系的是（ ）
A.y=x2
B.y=
C.y=x-3 D.y=
2.下列函数中,①y=πx ②y=2x-1 ③y=1/x ④y=2-3x ⑤y=x2-1中,是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
3.将函数y=x+2的图象向下平移3个单位,这时函数的解析式为（ ）:
A. y=x+5 B. y=3x+5 C. y=-3x+5 D. y=x-1
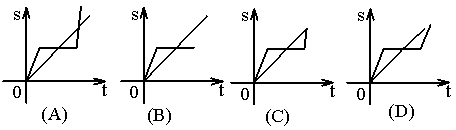
4.龟兔赛跑的故事是:乌龟和兔子进行赛跑比赛,它们同时从起点开始,跑了一段时间后兔子见乌龟被远远地落在后面,就躺下来休息一会儿,当它醒来时,发现乌龟已快到终点,于是向终点快速冲去,结果还是乌龟先到,下列图象符合题目意思的是( )
5.为加强公民节水意识,某市制定了用水收费新标准:每户每月用水未超过7吨,每吨收费1.0元,并加收0.2元的城市污水处理费;超过7吨的部分每吨收费1.5元,并加收0.4元的城市污水处理费.如果某单位共有用户50户,某月共交水费541.6元, 且超水户每月的用水量都未超过10吨,这个月用水未超过7吨的用户至少有( )
A.25户 B.26户 C.28户 D30户
6.已知一个一次函数的图象过点(-1,2),则这个一次函数的解析式可以是__________________
(只需写出一个解析式即可,不必考虑所有情况).
7.函数
中自变量的取值范围是___________________________
8.某种经营中利润是销售额的28%,设销售额为x万元,利润为y万元,其中常量是________,变量是________,y关于x的函数解析式是________________.
9.声音在空气中的传播速度v(米/秒)与温度t(℃)的关系可表示为:v=331+0.6t当t的值分别为-1,3时,相应的传播速度v的值为________,_________.
10.下列三个函数y=-2x,y=-
x,y=(
)x的共同点是(1)______________________;
(2)_______________________;(3)___________________________________.
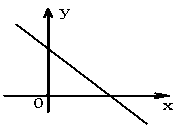
11.已知一次函数y=kx+b的图象如图所示,则k_______0,b______0
 |
12.一次函数y=kx+b表示的直线经过点A(1,2).B(-1,-4),试判断点P(2,5)是否在直线AB上.
13.已知y-5与x成正比例,且当x=-1时,y=8.
(1)写出y与x间的函数关系式;
(2)画出函数的图象;
(3)根据图象,求当x为何值时,y<0?
14.某地区现有果树12000棵,计划今后每年栽果树2000棵.
(1)求果树总数y(棵)与年数x (年)的函数关系式;
(2)预计到第5年该地区有多少棵果树?
15.鞋子的“鞋码”和鞋长（㎝）存在一种换算关系,下表是几组“鞋码”和鞋长的对应表:
| 鞋长 | 15 | 23 | 26 |
| 鞋码 | 20 | 36 | 42 |
(1) 通过画图.计算.比较.观察,猜想这种换算规律可能符合哪种函数关系?
(2) 设鞋长为x,鞋码为y,求y与x的换算关系式;
(3) 验证你所求的换算关系式是否正确;
(4) 如果我国著名篮球明星姚明的脚长31㎝,那么他应穿多大鞋码的鞋?
（二）能力活动
16.无论m为何实数,直线y=x+2m与y=-x+4的交点不可能在( )
A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限
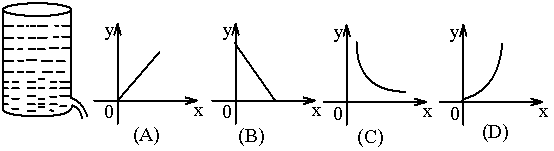
17.如图,圆柱形水箱内盛满水,水从水龙头流出,水箱内的水的高度y与放水时间x的关系适合下面的图象(设水的流速一定) ( )
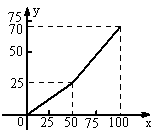18.为缓解用电紧张矛盾,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示:,
(1)根据图象请求出当0≤x≤50时,y与x的函数关系式_______________.
(2)当每月用电量不超过50度时,收费标准是____________________;
当每月用电量超过50度时,收费标准是____________________;
19.点A为直线y=-2x+2上的一点,点A到两坐标轴的距离相等,则点A的坐标为___________.
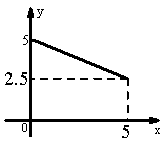20.如图是关于x的一次函数y=kx+b的图象,根据图象回答:
(1)自变量x的取值范围;
(2)当x取何值时,y的值最小?
(3)在(1)中x的取值范围内,y随的增大而怎样变化?
(4)求这个一次函数的解析式.
21.已知函数y=3x-6,若把其图象向上平移3个单位,得到另一条直线.
(1)求其移动后得到的直线解析式;
(2)在同一坐标系上画出两直线函数图象,并求出它们与x轴的交点坐标;
( 3)你能发现后一个函数的图象是由y=3x-6向左(或右)平移几个单位得到的?
22.某市电脑公司每月收取费用y元,与上网时间x(h)的函数关系如图所示,其中线段BA平行于x轴,AC是射线.
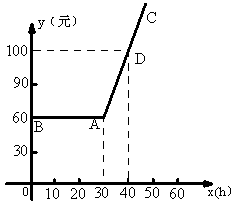(1)写出x≥30时,y与x之间的函数关系式.
(2)观察图象,请回答下列问题:
①某人一月上网20h,他应付多少元?
②当x取多少值,y=60?
③当x取哪些值时,y>60?
④当x取哪些值时,y<100?
23.某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元,小彬经常来该店租碟,若每月租碟数量为x张.
(1)写出零星租碟方式应付金额y1(元)与租碟数量x(张)之间的函数关系式;
(2)写出会员卡租碟方式应付金额y2(元)与租碟数量x(张)之间的函数关系式;
(3)小彬选取哪种租碟方式更合算?
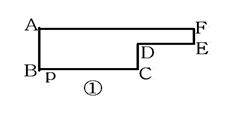
24.如图所示，已知动点P以每秒2㎝的速度沿图①的边框按从B→C→D→E→F→A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图②。若AB=6㎝，试回答下列问题：
（1）图①中BC的长是多少？
（2）图②中的a是多少？
（3）图①中的图形面积是多少？
（4）图②中的b是多少？
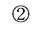
第十一章 一次函数(A)答案
一. 知识技能:
1.B 2.B 3.D 4.C 5.C 6.=-2x(答案不唯一) 7.x≠3 8.28%,x,y,y=28%x
9.330.4,332.8 10.都是正比例函数,随着x的增大y反而减少,图象都经过二、四象限.
11.k<0,b>0 12.y=3x-1,点P在直线AB上 13.y=-3x+5图略 x>5/3 14.y=12000+2000x,22000
15.①符合一次函数关系,②y=2x-10,③三组数据符合, ④52码
二. 能力活动:
16. C 17 .B 18①y=x ②0. 5元/度 ③0.9元/度 19.(2/3,2/3)(2,-2) 20.①0≤x≤5 ②当x=5时,y的值最小 ③y随x的增大而减少 ④y=-0.5x+5 21.①y=3x-3 ②(2,0) (1,0)③向左平移一个单位得到. 22.(1)y=3x-30(x≥30) (2)①60元 ②当0＜x≤30时, y=60 ③ 当x>30时y>60 ④ 当 x<130/3时 y<100 23.①y1=x ②y2=0.4x+12 ③当x>20时,选择会员卡合算,当x=20时,两种方式一样, 当x<20时,选择零星租碟合算 24.①8cm ②24cm ③60cm2 ④17