|
一、填空题（3、6题每空2分，10题5分，其它每题3分，共34分）
1．一个多边形的每个内角度数都是其外角度数的2倍，则这个多边形的边数是 ；
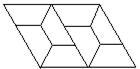2．如图是用形状、大小完全相同的等腰梯形密铺成的图案的一部分，这个图案中的等腰梯形的内角度数分别是
；
3．P（－3，－4）到y轴的距离是 ，关于y轴对称点的坐标是 。
4．电影院的8排10号用（8，10）表示，那么10排8号可用 表示。
5．若点A（-2，3）先向右平移3个单位，在向下平移1个单位，得到的点的坐标为_______________。
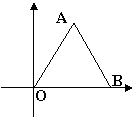
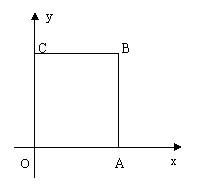
6.如图，等边△AOB是边长为6,则A，B两点的坐标分别是：A
，B
。
7．某函数具有下列两条性质：
(1)它的图象是经过点(1，－3)的一条直线．
(2)y的值随x值的增大而减小，请你举出一例满足上述两个条件的函数，
这个函数关系式可以是____________________________。
8．某商店出售一种瓜子，其售价y（元）与瓜子质量x（千克）之间的关系如下表
| 质量x（千克） | 1 | 2 | 3 | 4 | …… |
| 售价y（元） | 3.60+0.20 | 7.20+0.20 | 10.80+0.20 | 14.40+0.20 | …… |
由上表得y与x之间的关系式是 。
9．已知一次函数y=kx+5的图象经过点（-1，2），
则直线y＝kx经过 象限。
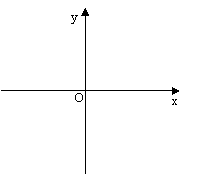
10．对于边长为4的正方形建立适当的直角坐标系,画在右图中，
并写出各点的坐标________________________________________
二、选择题（每题3分，共30分）
11．下列函数中，是一次函数，又是正比例函数，且y的值随x的增大而增大的是（ ）
A． y＝－2x－1 B． y＝2x－1 C．y＝－2x D． y＝2x
12．下面哪个点不在函数y=－2x+3的图象上（ ）
A．（－5，13） B．（0.5，2） C．（3，0） D．（1，1）
13．一次函数y= -2x+3的图象与两坐标轴的交点是( )
A．（3，0）（0，
） B．（3，0）（，0） C．（0，3）（，0） D．（0，3）（0，）
14．将平面直角坐标系内某个图形各个点的纵坐标都乘以－1，横坐标不变，所得图形与原图形的关系是：（ ）
A．关于x轴对称 B．关于y轴对称 C．关于原点对称 D．重合
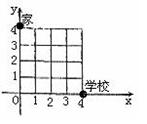15．如右图所示，小颖从家到达莲花中学要穿过一个居民小区，若小区的道路均是正南或正东方向，小颖走下面哪条线路不能到达学校（ ）
A． （0，4）→（0，0）→（4，0）
B． （0，4）→（4，4）→（4，0）
C． （0，4）→（1，4）→（1，1）→（4，1）→（4，0）
D． （0，4）→（3，4）→（4，2）→（4，0）
 |  | ||
16．
 |  | ||
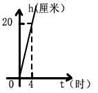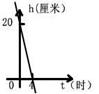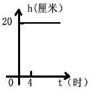
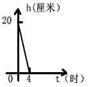
一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h (厘米)与燃烧时间t (时)的函数关系的图象是( )
A B C D
17．如图都是由若干盆花组成的形如三角形的图案，则组成第n个图案所需花盆总数y与n的关系式为（ ）
A． y=3n－1 B．y=3n
C． y=3n+1 D．y=3n+2
18．下列汽车标志中，是中心对称图形但不是轴对称图形的有（ ）个。
 | |||||||
 | |||||||
 | |||||||
 | |||||||
A．2 B．3 C．4 D．5
19．重庆市育才中学逸夫图书综合楼要铺设地面，已有正三角形
形状的地砖，现打算购买另一种不同形状的正多边形地砖，与正三角形地砖在同一顶点处作平面镶嵌，则该学校不应该购买的地砖形状是（ ）
A．正方形 B．正六边形 C．正八边形 D．正十二边形
20．正方形切去一角后，所得多边形的内角和为（ ）度．
A．540 B．360 C．180 D．180、360或540
三、解答题（共36分）
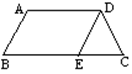21、（6分）如图，梯形ABCD中，AD∥BC, DE∥AB,
△DEC周长为12cm，BE=6cm，
求梯形ABCD的周长。
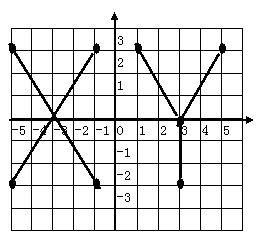
22、（6分）建立直角坐标系，标出以下各组点，并将各组内的点用线段依次连接起来，观察所得的图形，你认为它是什么？
①(-5,3),(-1,-3)； ②(-1,3),(-5,-3)
③(1,3),(3,0),(5,3)； ④(3,0),(3,-3)
23、（8分）如图，lA、 lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系。
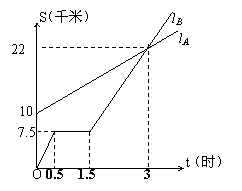（1）B出发时与A相距
千米。（1分）
（2）走了一段路后，自行车发生故障，进行
修理，所用的时间是 小时。（1分）
（3）B出发后 小时与A相遇。（2分）
（4）求出A行走的路程S与时间t的函数关系式。
（写出过程，4分）
24．（8分）某公司要印制新产品宣传材料。甲印刷厂提出：每份材料收1元印制费，另收1500元制版费；乙厂提出：每份材料收2.5元印制费，不收制版费。
(1)分别写出两厂的收费
(元)与印制数量
(份)之间的关系式；(2)在同一直角坐标系内作出它们的图象；(3)根据图象回答下列问题：印制800份宣传材料时，选择哪家印刷厂比较合算？这家公司拟拿出3000元用于印制宣传材料，找哪家印刷厂印制宣传材料能多一些？
25．（8分）对于气温，有的地方用摄氏温度表示，有的地方用华氏温度表示，摄氏温度与华氏问题之间存在着某种函数关系。从温度计的刻度上可以看出，摄氏(℃)温度x与华氏(℉)温度y有如下对应关系：
(1)请你画出直角坐标系，描出相应的各点，并将各点依次用线段连结起来；(2)请通过①猜测②求解③验证等步骤确定华氏温度y(℉)与摄氏温度x(℃)之间的函数关系式； (3)某天青岛的最高气温是8℃，澳大利亚悉尼市的最高气温是91℉，问这一天悉尼的最高气温比青岛的最高气温高多少(结果保留整数)?
参考答案：
一、
1．6 2．60°、60°、120°、120° 3．3；（3，－4） 4．（10，8） 5．（1，2） 6．A（3，3
）；B（6，0）
7．y＝－x－2，y＝－2x－1等 8．y＝3.60x＋0.20
9．一、三 10．分别以正方形的一组邻边为x轴、y轴，如图所示建立平面直角坐标系。
A（4，0）B（4，4）C（0，4）O（0，0）
二、
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | D | C | C | A | D | D | B | A | C | D |
三、
21．24cm
22．
XY
23．
(1)10
(2)1
(3)3
(4)解：设直线lA的函数关系式为：S=kt＋b
由题意得b＝10,3k＋b＝22
∴b＝10，k＝4
∴S＝4t＋10
24．
见教材习题6.7
25．
（1）图略
（2）y＝1.8x＋32
（3）45℉或25℃
试题命制双向细目表
| 知识点 | 内容 | 总计 | 百分率 | |||
| 填空题 | 选择题 | 解答题 | ||||
| 第四章 （21） | 梯形 | 2 | 21 | 9 | 9％ | |
| 多边形的内角和与外角和 | 1 | 20 | 6 | 6％ | ||
| 平面图形的密铺 | 19 | 3 | 3％ | |||
| 中心对称图形 | 18 | 3 | 3％ | |||
| 第五章 （31） | 确定位置 | 4 | 3 | 3％ | ||
| 平面直角坐标系 | 3、6、10 | 22 | 19 | 19％ | ||
| 图形与坐标变换 | 5 | 14、15 | 9 | 9％ | ||
| 第六章 （48） | 函数 | 8 | 17 | 6 | 6％ | |
| 一次函数 | 11 | 3 | 3％ | |||
| 一次函数图像 | 9 | 12、13、16 | 12 | 12％ | ||
| 确定一次函数表达式 | 7 | 23 | 11 | 11％ | ||
| 一次函数图像应用 | 24、25 | 16 | 16％ | |||