2005年度八年级（上）数学月评价试卷
一．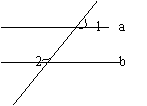 
基本知识与基本技能（本题有10小题，共30分）．
1．如图a∥b，∠1=45°，则∠2= 。
2、点A(-1,3)关于y轴对称的点的坐标是___________
3．在Rt△ABC中，∠C=90°，AB=15㎝，D是AB边的中点，则CD= 。
4．为了了解全国青少年的上网情况作调查，你将采用什么调查方式？
答： ______
5．在函数y=
中,自变量的取值范围是
________ 。
6.点P(-5,1)沿x轴正方向平移2个单位,再沿y轴负方向平移4个单位,所得到的点的坐标为_______ .
7．三角形三边长分别为4，1-2a，7，则a的取值范围是
8．不等式
的正整数解为___________________
9．写一个图象经过点（－1，2），并y随x的增大而增大的一次函数的解析式_______________
10.已知关于x的不等式组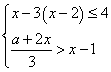
的解集是
，
则a=_________
二、谁的命中率高（本题有10小题，共30分）．
11．以下各组数中，能组成直角三角形的是（ ）
(A)2，3，4 (B)1.5，2，2.5 (C)6，7，8 (D)8，9，10
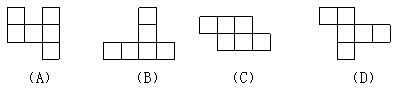12．下列各图中能折成正方体的是( )
|
的年龄统计结果如右表所示：
则此班学生年龄的众数、中位数分别为（ ）
（A）．14，14 （B）．15，14 （C）．14，15 （D）．15，16
14.若a＞0,b＜-2,则点(a,b+2)应在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
15.已知x轴上的点P到y轴的距离为3,则点P的坐标为( )
A.(3,0) B.(0,3) C.(0,3)或(0,-3) D.(3,0)或(-3,0)
16．已知不等式组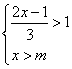
的解集为
，则( )
17．已知点A(a+2,5)、B(-4,1-2a),若直线AB平行于x轴,则a的值为( )
A.-6 B.2 C.3 D.-2
18．下列各点中，不在函数y=2x+1的图象上的是 ( )
(A) ( 0, 1 ) (B) ( 1, 3 ) (C) ( -
, 0 ) (D) ( -1, 3 )
19．若直线y=kx+b经过第一、二、四象限，则k,b的取值范围是 （ ）
(A) k>0, b>0 (B) k>0,b<0 (C) k<0,b>0 (D) k<0,b<0
20．一水池蓄水20
，打开阀门后每小时流出5，放水后池内剩下的水的立方数Q（）与放水时间t（时）的函数关系用图象表示为 （ ）
Q
Q
Q
Q
20 20 20 20
4 t 4 t 4 t 4 t
(A) (B) (C) (D)
三．解答题（21～24题，每题6分，25～26题，每题8分）
21．已知一次函数的图象经过点A(-3,4), B(-1,-2).
（1）求出这个一次函数的解析式，并作出它的图象
（2）求△AOB的的面积.
（3）由图象观察，当-4≤x≤1时，函数y的变化范围
22．解不等式组，并在数轴上表示解集。
⑴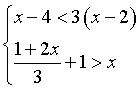
 |
23．画出右图几何体的三种视图。
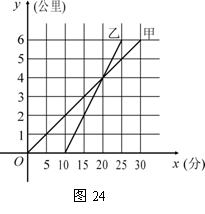24．甲骑自行车、乙骑摩托车沿相同路线由A地到B地，行驶过程中路程与时间的函数关系的图象如图： 根据图象解决下列问题：
(1)谁先出发？先出发多少时间？谁先到达终点？
先到多少时间？
(2)分别求出甲、乙两人的行驶速度；
(3)在什么时间段内，两人均行驶在途中(不包括起点和终点)？
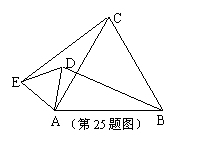25.如图所示,若△ABC、△ADE都是正三角形，请试比较：线段BD与线段CE的大小？写出你的猜想，并说明理由.
26．某中学八年(12)班同学利用勤工俭学收入的66元钱，同时购买单价分别为3元、2元、1元的甲、乙、丙三种纪念品，奖励参加校“元旦会演”活动的同学。已知购买乙种纪念品件数比购买甲种纪念品的件数多2件，而购买甲种纪念品的件数不少于10件，且购买甲种纪念品的费用不超过总费用的一半，若购买的甲、乙、丙三种纪念品恰好用了66元钱，问可有几种购买方案？每种方案中购买的甲、乙、丙三种纪念品各有多少件？