初二年数学期末测查参考试卷（二）
（考试时间：120分钟， 满分150分）
班级 座号 姓名 成绩
一、填空题（1—11题每题3分，第12题6分，共39分）
1、计算:（－3ab3）2= 。
2、“a，b两数的平方和不是负数”用不等式表示为 。
3、四边形ABCD中，已知AB=CD，若要使它成为平行四边形，则还需添加的一个条件可以是 。
4、火车在一段笔直的铁轨上行驶，我们可以把它看成是火车沿着铁轨的方向移动了一定距离，这就是平移。请你再举出生活中的一个平移的例子：
。
5、你注意过教室里的电风扇吗？电风扇的叶片至少转动 度后才能与自身重合。
6、（ ）（－a+b）=a2－b2。
7、已知矩形一对角线长是12cm，它与一边的夹角为60°，则矩形较短的一边边长为 cm。
8、多项式1+4x 2加上一个单项式后，就能成为一个完全平方式，请你试一试并填空：1+4x 2+ =（ ）2
9、如果（x－2）（x +4）= x 2－m x－8，则m = 。
10、某灯泡厂一次质量检查中，从300个灯泡中抽查了50个，其中有3个不合格，则出现不合格灯泡的频率是 ，在这300个灯泡中估计有 个为不合格产品。
11、已知不等式组
（其中a
>1），则这个不等式组的解集是
。
12、（本题每一空格1分）
（1）比较下列算式结果的大小：
42+32 2×4×3， （－2）2+12 2×（－2）×1，
242+
2×24×
， 22+22 2×2×2
通过观察、归纳，比较：20032+20042 2×2003×2004
（2）请你用字母a、b写出能反映上述规律的表达式： 。
二、选择题（每小题4分，共24分；每小题有且只有一个正确答案）
13、用两个完全相同的直角三角形拼下列图形：
①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 ⑥等边三角形，
一定可以拼成的图形是………………………………………………（ ）
A.①④⑤ B.②⑤⑥ C.①②③ D.①②⑤
14、用120根火柴，首尾相接围成一个三条边互不相等的三角形，已知最大边是最小边的3倍，则最小边用了 ……………………………………（ ）
A.20根 B.19根 C.18根或19根 D.19根或20根
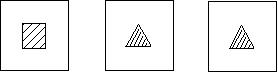
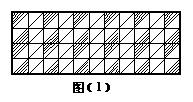15、一只蚂蚁在如图（1）所示的黑白相间的地板上行走，如果停下来休息，那么可以估计它所停的位置为黑色部分的机会是 （ ）
A.
B.
C.
D.
16、下列各小题：
①（5×103）×（2×102）=1×106， ②415＜168， ③0.2510×410=1，
④（2a－3c）（－3c－2a）=9c2－4a 2 ⑤ （－m－n）2=m 2+2mn+n 2
其中正确的有…………………………………………………………（ ）
A、①②③④⑤ B、①③④⑤ C、①④ D、②③⑤
17、已知菱形ABCD，∠A=72°，将它分割成如图（2）所示的四个等腰三角形，则∠1，∠2，∠3，的度数分别是…………………………………（ ）
A.36°，54°，36° B.18°，54°，54°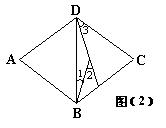
C.18°，36°，36° D.54°，18°，72°
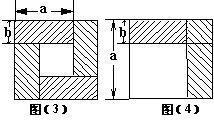18、我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式。例如图（3）可以用来解释（a +b）2－（a－b）2=4
ab。那么通过图（4）面积的计算，验证了一个恒等式，此等式是………………………（ ）
A. a 2－b2=（a +b）（a－b）
B.（a－b）（a +2b）= a 2+ ab－b 2
C.（a +b）2= a 2+2 ab+b 2
D.（a－b）2= a 2－2 ab+b 2
三、实践题（各6分，共12分）
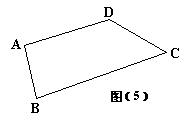19、现有一把木工师傅专用的曲尺（两边互相垂直且有刻度），你能用这把尺来检查一块四边形木板ABCD的一组对边BC与AD是否平行？如果能，说明你的办法；如果不能，说明理由。
20、观察图（6）和图（7），请回答下列问题：
（1）请简述由图（6）变成图（7）的形成过程： 。
（2）若AD=3， DB=4，则△ADE和△BDF面积的和为 。
四、计算题（各6分，共18分）
21、先化简，再求值。
3
x（x 2－x－1）－（x +1）（3 x 2－x），其中x =－
22、解不等式组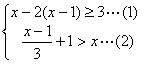
，并把解集在数轴上表示。
23、分解因式：x 3（x－y）+ x（y－x）
五、解答题（1、2题各7分，3题9分，共23分）
24、a取何值时，关于x的方程2 x－2a= x－（3a +2）的解不是正数？
25、一个正方形的边长增加3cm，面积增加39cm2，求这个正方形的边长。
26、平行四边形ABCD中，对角线AC，BD相交于O，若E，F是AC上两动点，分别从A，C两点以相同的速度 1cm/s 向C、A运动，
（1）四边形DEBF是平行四边形吗？说明理由；
（2）若BD=12cm，AC=16cm，当运动时间t 为何值时，四边形DEBF是矩形？
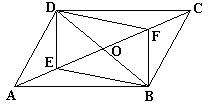
图（8）
六、探究题（1、2题各12分，3题10分，共34分）
27、在西湖公园的售票处贴有如下的海报：
（1）如果八年级（1）班27名同学去西湖公园开展活动，那么他们至少要花多少钱买门票？
（2）你能针对该班参加活动各种可能的人数，设计合理的买票方案吗？
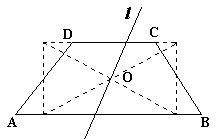
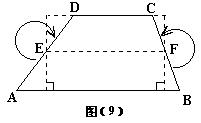28、任意剪一个梯形纸片，利用对折的方法找到腰的中点E、F，按图（9）中所示的方法分别将含∠A，∠B的部分向里剪下①，②，并图中箭头所示的方向旋转180°，
①你能得到一个怎样的四边形？
②你能发现关于线段EF的哪些特性？
③请你画出一条直线，将梯形ABCD分成面积相等的两部分（保留作图痕迹），这样的直线你能画几条？简要说明你的想法。
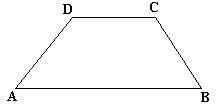
29、在拼图游戏中，把下图中三张纸片放在盒子里搅匀，任取两张看看能拼成菱形还是能拼成房子。想一想，有哪些方法可用模拟实验？尽可能多地说出你的方法，并分别估计拼成菱形和拼成房子的机会。
初二年（上）数学期末考试卷（二）参考答案
一、填空（39分）
1、9 a 2b6 2、a 2+b2≥0 3、AB∥CD（或AD=BC） 4、电梯工作时，等
5、120° 6、－a－b 7、6 8、－1，±4 x，4 x 4
9、2 10、6% 18 11、无解 12、①＞ ＞ ＞ ＝ ＞
②a 2+b2≥2 a b
二、选择题（24分）
13～18：D、C、C、A、C、D
三、实践题（共12分）
19、能，将曲尺一边卡住BC（或AD）使曲尺边与四边形边重合，再利用刻度读出曲尺与对边相交时的长度，变换位置，重复一次做法，各长度相等，即AD与BC平行，如不相等，即不平行。
20、（1）把△DFA'绕点D顺时针方向旋转90° （2）6
四、计算题（18分）
21、原式=－x 2－2 x，当x =－时，原式=
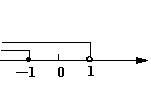
22、由①得x≤－1，由②得x＜1
∴原不等式组解集x≤－1
23、原式= x（x－y）（x +1）（x－1）
五、解答题（共23分）
24、解关于x的方程，得x =－a－2，
依题意得－a－2≤0，a≥－2，
∴当a≥－2时，原方程的解不是正数。
25、设这个正方形边长x cm，
则（x +3）2－x 2=39，
解得x=5，
答：略
26、（1）∵四边形ABCD是平行四边形
∴AO=CO BO=DO ，
当E、F分别从A、C两点以相同速度运动时，CF=AE恒成立，
由于AO－AE=CO－CF（当E、F运动至OC、OA上，有AE－AO=CF－CO）
即OE=OF，
∴当E、F不与O重合时，由OE=OF，DO=BO可得四边形DEBF是平行四边形，当E、F与O重合时，不是平行四边形
（2）当t=2s或t=14s时，EF=BD，平行四边形为矩形。
六、探究题（共34分）
27、至少要花120元；
②当参加活动人数少于24人时，选择买个人票合算；当人数为24时，买个人票与团体票一样合算；当人数超过24人时，选择买团体票合算。
28、①矩形 ；
②EF与上下底DC、AB平行，且等于AB、CD和的一半。
③直线l为所求的。可以画无数条。如图，过两腰中点画与两底构成的矩形，矩形对角线交于O，过O点且过DC上一点的直线为所求的。
29、模拟实验方法：略
拼成菱形的机会
，拼成房子的机会
。