初二几何（下）单元测试（五）
相似三角形、三角形相似的判定、相似三角形的性质、相似多边形
班级________姓名________座号________成绩________
一、填空题（每小题3分，共30分）
1．如图（1-1）点E、C分别在AB、AD上，BC与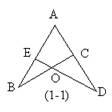
DE相交于O，若∠B=∠D，图中有________对相似三角形。
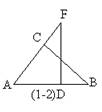
2．
如图（1-2）：BC⊥AF，FD⊥AB，垂足分别为C、D，那么，图中有________对相似三角形。
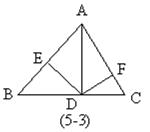
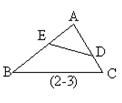
3．
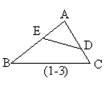如图（1-3）：已知∠ADE=∠B，则⊿____∽⊿____，
4．
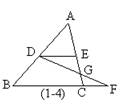
如图（1-4）：已知DE∥BC，DF交AC于G，则图中的相似三角形有：
⊿____∽⊿____，⊿____∽⊿____。
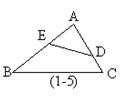
5．如图（1-5）：DE不平行于BC，当AB∶AE=（ ）∶（ ）时，⊿ABC∽⊿AED。
6．
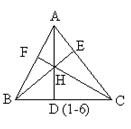
如图（1-6）：在⊿ABC中，AD⊥BC，BE⊥AC，CF⊥AB，三高相交于点H与⊿BDH相似的三角形有____个。
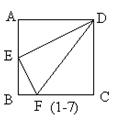
7．如图（1-7）：正方形ABCD中，E为AB的中点，FC=3BF，那么与⊿AED相似的三角形有_____________________
______________________________。
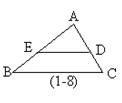
8．如图（1-8）：D、E分别为⊿ABC的AB、AC边上的点，⊿ADE∽⊿ABC，∠B=∠ADE，AD∶DB=3∶2，则DE∶BC=________。
9．
已知CD是Rt⊿ABC斜边AB上的高，且AC=6cm，AB=10cm，则AD=________cm。
10.顺次连结三角形三边中点所成三角形的面积与原三角形的面积比为____________。
二、 判断题（对的填A，错的填B，共10分）
1．两个全等三角形一定是相似三角形。（ ）
2．两个等腰三角形一定是相似三角形。（ ）
3．如图（2-3）：已知⊿ABC∽⊿ADE，其中∠ADE=∠B，则
。（ ）
4．一个三角形两角分别是60o，72 o，另一个三角形的两角，分别是600、480，这两个三角形相似。（ ）
5．如果⊿MNP∽⊿DEF，那么∠M=∠D，∠N=∠E，∠P=∠F，且
。（ ）
三、
选择题（共18分）
1．在下列图形中，必成相似三角形的是（ ）。
(A) 有一个角为30 o的两个等腰三角形
(B)邻边的比为2的两个平行四边形
(C)底角是40 o的两等腰梯形
(D)有一个角是1200的两个等腰三角形
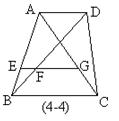
2．如图：已知梯形ABCD中，AD∥BC，对角线AC、BD相交于O，腰BA、CD的延长线相交于M，图中相似三角形共有（ ）对。
(A)1 (B)2 (C)3 (D)4
3．
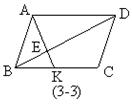如图：已知平行四边形ABCD中，K是BC上一点，且
，AK交BD于E，则图中的相似三角形的相似比是（ ）。
(A)⊿BAD∽⊿BEK，相似比为3∶7
(B)⊿BEK∽⊿BCD，相似比为3∶7
(C)⊿BEK∽⊿BEA，相似比为3∶7
(D)以上各结论都不对
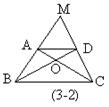
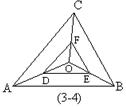
4．如图：O为⊿ABC内一点，D、E、F分别是OA、OB、OC的中点，图中相似三角形有（ ）。
(A)2对 (B)3对 (C)4对 (D)5对
5．如果点D为⊿ABC的BC边上的点，则下列条件不能判定⊿ACD和⊿BCA相似的是（ ）。
(A)∠CAD=∠B (B)∠ADC=∠BAC
(C)AC2=BC·DC (D)∠C=∠BAC
6．若两个相似多边形的周长分别为80cm和140cm，它的面积的和为130cm2，则这两个多边形的面积分别为（ ）。
(A)47cm2和83cm2 (B)47.2cm2和82.8cm2
(C)32cm2和98cm2 (D)以上答案都不对
四、 计算题（每小题5分，共20分）
1．已知：⊿ABC∽⊿EFG，若∠A=27 o，∠F=48 o，求∠C的度数。
2．如图：已知等边⊿ABC，正方形内接于⊿ABC，AB=2，求正方形的边长。
3．已知：⊿ABC中，∠C=900，D是AB的中点，DE∥BC交BC于E，
DF∥BC，交AC于F，若AB=5，AC=3，求四边形DECF的周长。
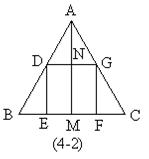
4．
如图：已知AD∥EG∥BC，AD=6，BC=9，
，求GF的长。
五、 证明题（共22分）
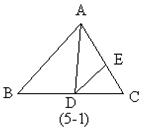
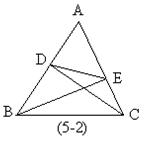
1．如图：已知在⊿ABC中，
，E是AC上的一点，且AC=6cm，CE=
cm，
，求证：⊿CDE∽⊿CBA（7分）
2．如图，在⊿ABC中，CD⊥AB于D，BE⊥AC于E，连结DE，
求证：∠AED=∠B（7分）
3．如图：已知在⊿ABC中，AD⊥BC于D，DE⊥AB于E，DF⊥AC于F，
求证：AE·EB=AF·FC（8分）
