八年级期中考试
一、填空题：（3分×8=24分）
1、
－π=__________.
2、若
，则ab=__________.
3、
，则a的值为__________.
4、比较大小：
（1）cos89°_________cos19° （2）cos10°_________sin20°.
5、已知一次函数y=－mx＋(m－2)，若它的图象经过原点，则m=_________；若图象经过一、三、四象限，则m的
取值范围是__________.
6、公民的月收入超过800元时，超过部分须依法缴纳个人收入调节税，当超过部分不足500元时，税率（即所纳
税款占超过部分的百分数）相同.已知某人某月收入1260元，纳税23元，由此可得所纳税款y（元）与该人月
收入x（元）（800<x<3000）之间的函数关系是__________.
7、若sinα＋cosα=m，则sinα－cosα（0°<α<45°）=__________.
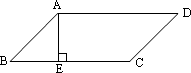
8、如图，在菱形ABCD中，AE⊥BC于E，EC=1，sinB=
,则四边形AECD的周长=__________.
二、单项选择题：（3分×8=24分）
9、下列语句中正确的是（ ）
A．带根号的数是无理数 B．不带根号的数一定是有理数
C．无理数一定是无限不循环小数 D．无限小数都是无理数
10、若点A关于x轴的对称点的坐标为（－1，2），则A点的坐标是（ ）
A．（－1，－2） B．（1，2）
C．（1，－2） D．（－1，2）
11、函数y=－3x＋4的图象不经过（ ）
A．第一象限 B．第二象限
C．第三象限 D．第四象限
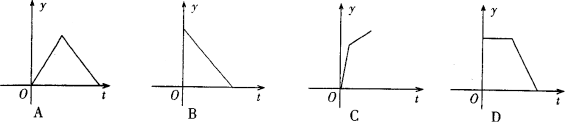
12、某产品的生产流水线每小时可生产100件产品，生产前没有产品积压，生产3h后安排工人装箱，若每小时装
产品150件，未装箱的产品数量y是时间t的函数，这个函数的大致图象只能是下图中的（ ）
13、如果∠A为锐角，且cosA=
,那么（
）
A．0°<∠A
30° B．0°<∠A45°
C．45°<∠A60° D．60°<∠A90°
14、如图所示，下列每个图是由若干盆花组成的形如三角形的图案，每条边（包括两个顶点）有n盆花，每个图
案花盆总数是S，按此推断S与n的关系式为（ ）
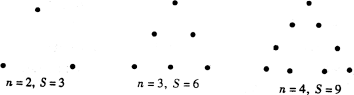
A．S=3n B．S=3(n－1)
C．S=3n－1 D．S=3n＋1
15、下列函数中自变量x的取值范围是x
2的是（
）
A．y=
B．y=
C．y=
D．y=
16、幸福村村办工厂今年前五个月生产某种产品的总量C（件）关于时间t（月）的函数图象如图所示，则该厂对
这种商品来说（ ）
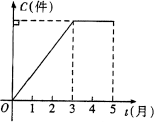
A．1月至3月每月生产总量逐月增加，4、5两月每月生产总量逐月减少
B．1月至3月每月生产总量逐月增加，4、5两月每月生产量与3月持平
C．1月至3月每月生产总量逐月增加，4、5两月均停止生产
D．1月至3月每月生产总量不变，4、5两月均停止生产
三、解答题
17、（6分）下列各式中哪些是同类二次根式
（1）
，
，
，
，
，
，
（2）5
，
，
，
18、（6分）当k为何值时，函数y=(k2＋2k)
是正比例函数？
19、（6分）（1）若点（5－a,a－3）在第一、三象限角平分线上，求a的值；
（2）已知两点A（－3，m），B（n,4），若AB∥x轴，求m的值，并确定n的范围；
（3）点P到x轴和y轴的距离分别是3和4，求点P的坐标；
（4）已知点A（x,4－y）与点B（1－y,2x）关于y轴对称，求yx的值.
20、（6分）已知：在Rt△ABC中，∠C=90°，cosA=
,求sinA的值；
21、（8分）已知如图，四边形ABCD是菱形，AF⊥AD交BD于E，交BC于F.
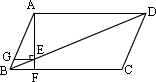
（1）求证：AD2=
DE·DB；
（2）过点E作EG⊥AF交AB于点G，若线段BE、DE（BE<DE）的长是方程
（m>0）的两个
根，且菱形ABCD的面积为6，求EG的长.
22、（8分）某房地产集团筹建一小区，居民楼均为平顶条式，南北朝向，楼高统一为16m（五层）.已知该城市
冬至正午时分太阳高度最低，太阳光线与水平线的夹角为32°，如果南北两楼相隔仅有20m（如图所示），
试求：
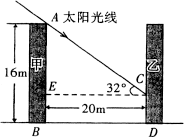
（1）此时南楼的影子落在北楼上有多高？（已知tan32°=0.6249）
（2）如按城市规划要求，使前后楼每层居民在冬天都能有阳光，两楼间的距离应是多少米？
23、（8分）在△ABC中，（1）若∠C=90°，cosA=
，求sinB的值；
（2）若∠A=35°，∠B=65°，试比较cosA与sinB的大小；
（3）若此三角形为任意锐角三角形，能否判断cosA＋cosB＋cosC与sinA＋sinB＋sinC的大小？若能，证明
你的结论；若不能，请说明理由.
24、（8分）阅读下列材料，按要求解答问题：
（1）观察下面两块三角尺，它们有一个共同的性质：∠A=2∠B，我们由此出发来进行思考.
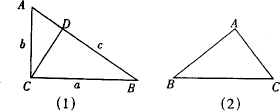
在图（1）中，作斜边上的高CD，由于∠B=30°，可知c=2b,∠ACD=30°，于是AD=
，BD=c－.
由于△CDB∽△ACB，可知
=
，即a2=c·BD,同理b2=c·AD.于是，
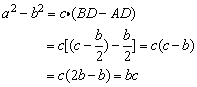
对于图（2），由勾股定理a2=b2+c2，
由于b=c,∴a2－b2=bc.
这两块三角尺都具有性质a2－b2=bc.
在△ABC中，如果一个角等于另一个内角的2倍， 我们称这个三角形为倍角三角形，两块三角尺就都是特殊的倍角三角形。对于任意的倍角三角形，上面的性质仍然成立吗？
如图（3），在△ABC中，若∠CAB=2∠ABC，则a2－b2=bc.
在上述由三角尺的性质到“猜测”这一认识过程中，用到了下列四种数学思想方法中的哪个？
选出一个正确的将其序号填在括号内（ ）
①分类的思想方法； ②转化的思想方法；
③由特殊到一般的思想方法； ④数形结合的思想方法.
（2）这个猜测是否正确？请证明.
25、（8分）如图（1）所示，四边形ABCD是一张矩形纸片，∠BAC=α
（0°<α45°），现将其折叠，使A、C二点重合.
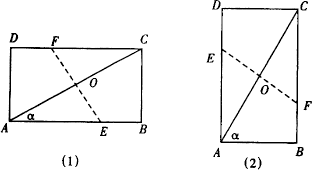
（1）作出折痕EF；
（2）设AC=x，EF=y，求出y与x之间的函数关系式；
（3）如图（2），当45°<α<90°时，（2）中求得的函数的关系式是否成立？若成立，请说明理由；若不
成立，请求出当45°<α<90°时，y与x之间的函数关系式.
26、（8分）为了预防“非典”，某学校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气
中的含药量y(mg)与时间x(min)成正比例，药物燃烧完后，y与x成反比例（如图所示）.现测得药物8min燃
毕，此时室内空气中每立方米的含药量为6mg，请根据题中所提供的信息，解答下列问题：
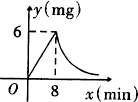
（1）药物燃烧时，y关于x的函数关系式为_________，自变量x的取值范围是：___________；药物燃烧后，
y关于x的函数关系式为：__________；
（2）研究表明，当空气中每立方米的含药量低于1.6mg时学生方可进教室，那么从消毒开始，至少需要经过
_________min后，学生才能回到教室；
（3）研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的
病菌，那么此次消毒是否有效？为什么？