华师大版2006年初二数学竞赛试题练习题(1)

2006年初二数学竞赛试题练习题(1)

　　　　命题人：亲新　 要答案请与本人联系号码：

一、　　　　　　 选择题 （每题5分，共35分）

1．下列四个数中等于100个自然数之和的是(　　 )

A、　 B、　C、　 D、

2．在体育活动中，初二（7）班的n个学生围成一圈做游戏，与每个学生左右相邻的两个学生的性别不同，则n的取值可能是（　　）

A、 43　　 B、44　　  C、45　　　　D、 46

3．三角形ABC中，AB=AC，BE⊥AC，D是AB的中点，且DE=BE，则∠C的度数是（　 ）

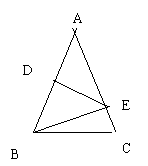A、65⁰　  B、70⁰　 C、75⁰　　D、80⁰　

4．已知a-b=4,ab+c²+4=0则a+b=(　　 )

A、4　　 B、0　　 C、2　　  D、-2

5.若a,b是正数,且满足12345=(111+a)(111-b)则a与b之间的大小

　关系是（　　）

A、a>b　 B、a=b　C、a<b　 D、不能确定

6．化简（　　）

A、　B、　C、　 D、

7．设a,b是正整数，且满足56≤a+b≤59，0.9＜＜0.91,则b²-a²等于 (　　  )

A.171　　　B.177　　　　　　 C.180　　　　　 D.182　

二、填空题（每题5分，共35分）

1．已知是正整数，并且，则=　　　。

2．如果a=2006x+2007,b=2006x+2008,c=2006x+2009,那么代数式a²+b²+c²-ab-ac-bc

的值等于________

3．分解因式：=　　　　　　　　　　　　　　  。

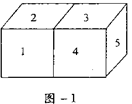4．两个同样的正方体拼在一起如图所示，每个正方体上相对的两个面上的数字之和都等于－2，现两个并列放置的正方体组成的几何体上看得见的五个面上的数字如图所示，则看不见的七个面上的数字之和为___________.

　　　　　　　　　　　　　　　　　 

5．某汽车从A地驶向B地，若每分钟行驶千米，则11点到达，若每分钟行驶千米，则11：20时距离B地还有10千米；如果改变出发时间，若每分钟行驶千米，则11点到达，若每分钟行驶千米，则11：20时已经超过B地30千米。A、B两地的路程是____千米。

6．如果正整数有以下性质：的八分之一是平方数，的九分之一是立方数，它的二十五分之一是五次方数，那么就称为“希望数”，则最小的希望数是_____。

7．一个一次函数图象与直线平行，与x轴、y轴的交点分别为A、B，并且过点（－1，－25），则在线段AB上（包括端点A、B），横、纵坐标都是整数的点有_____________个。

三、解答题(每题20分，共40分)

1．在中，是上一点，M是CD的中点，若，求证：。

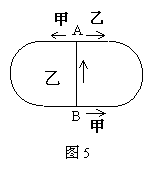
2．图5是一个长为400米的环形跑道，其中A、B为跑道对称轴上的两点，且A、B之间有一条50米的直线通道，甲、乙两人同时从A点处出发，甲按逆时针方向以速度沿跑道跑步，当跑到B点处时继续沿跑道前进，乙按顺时针方向以速度沿跑道跑步。当跑到B点处时沿直线通道跑回到A点处，假设两人跑步时间足够长。求：

　　（1）如果，那么甲跑了多少路程后，两人首次在A点处相遇？

（2）如果，那么乙跑了多少路程后，两人首次在B点处相遇？