初中数学夏令营赛前模拟试题（12）

初中数学夏令营赛前模拟试题（十二）

第 一 试

1. 设a、b、c、x、y、z都是实数, 且同时满足a²+b²+c²=25,　x²+y²+z²=36, ax+by+cz =30, 则= __________.

2. 不等式>2对一切x都成立, 则k的取值范围为___________.

3. 预计用1500元购买甲商品x个, 乙商品y个, 不料甲商品每个涨价1.5元, 乙商品每个涨价1元, 尽管购买甲商品的个数比预定数少10个, 总金额仍多用29元, 又若甲商品每个只涨价1元, 并且购买甲商品的数量只比预定数少5个, 那么甲乙两商品支付的总金额是1563.5元, 若预计购买甲商品的个数的2倍与预计乙商品的个数的和大于205, 但小于210, 则x = _______,y = ___________.

4. 计算:

5. 已知x是任意实数, a <z, 则函数 y = 的最值为__________.

6. 在黑板上从1开始, 写出一组相继的正整数, 然后擦去了一个数, 其余的平均值为35, 则擦去的数为________.

7. 正方形ABCD的边长为a, E是DC上一点, DE的长为b,　AE的中垂线与AD、AE、BC分别交于P、M、Q, 则PM:MQ= 　　　　　　　.

8. 等腰Rt△ABC中, D为斜边AB的中点, E、F分别为腰AC、BC上(并于端点)的点, DE⊥DF, AB=10, 设x=DE+DF, 则x的取值范围为______.

9. 在 △ABC中, ∠C = 90° , ∠A 的平分线AD交BC于D, 则 = _________.

10. 设M、N分别是△ABC两边AB、AC的中点, P是MN上任意一点,延长BP交AC于点Q, 延长CP交AB于R, 则= ________.

第 二 试

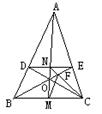
1. 如图, 在△ABC中, DE∥BC, 且DE=BC, BE与CD相交于点O, AO与BC、DE分别交于点M、N, CN与BE交于点F, 连结FM, 求证: FM= AB.

2. 试求出所有的整数k, 使得x的一元二次方程 kx²－2(3k－1)x+9k－1=0 的某一根是一个分母为1999的既约分数.

3. 求使得不等式 x²+px+q ≤z, 当1≤x ≤5时恒成立的实数对(p, q).