初中数学夏令营赛前模拟试题（十一）
第一试
1. 方程组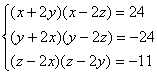
的解为__________________.
2. 已知 a、b、c是正整数, 方程ax2+bx+c=0 有两个不同实根, 且x1＜1, x2＜1, 则a+ b+ c的最小值为_____________.
3. 已知a＋2b＋3c=6, 则a2＋2b2＋3c2的取值范围是_______________.
4. P是⊙O内一点, ⊙O的半径是15, OP = 9, 则过P点且长度是整数的弦共有_______条.
5. 有一人利用休假的四个城市a、b、c、d旅游, 他今天在这个城市, 明天又到另一个城市, 请问该同志从a城出发5天后又回到a城的不同旅游线路有_________条.
6. 自然数a1, a2, …, a10的和为1001, d为a1, a2……, a10的最大公约数, 则d的最大值为___________.
7. 已知ABCD是圆内接四边形, 两组对边延长后分别交于E, F, 且EA·ED = 25, FC·FD = 144, 则EF = _________.
8. 平面上有n个点, 其中任意三点作成的三角形的面积都小于1, 若这n个点在△ABC内, 也可以在边上, 则△ABC的最小面积小于____________.
9. 已知a是正实数, 方程
的解是__________.
10. 设a、b都是自然数, 当a2＋b2除以a＋b时, 商是q, 余数是r, 且满足q2＋r = 1997, 则这样的a, b共有_________组.
第二试
1. 设a, y, z是实数, 且满足x＋y＋z = 0, xyz = 2, 求x＋y＋z的最小值.
2. 等腰Rt△ABC中, ∠A = 90°, 点D和E为边BC上的点, 且∠DAE = 45°,△ADE的外接圆分别交边AB和AC于点P和Q, 求证: BP＋CQ=PQ.
3. 已知a1,
a2, …, an, b1, b2,
…, bn是zn个正数, 且
, 
, 试证: n个分数
, 
, …, 
中的最小数一定不大于1.