初中数学夏令营赛前模拟试题（十）
第一试
1. 设A、B在直线l的同侧, 已知AB=13, 点A、B到直线l的距离分别为10.5和5.5点C是l上使AC＋BC最小的点, 则AC＋BC = ___________.
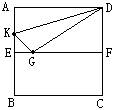
2. 如图, EF是正方形ABCD的对折线, 将∠A
沿DK折叠, 使它的顶点A落在EF上的G点, 则
∠DKG=____________度.
3. 设P为□ABCD内一点, ∠BAP =∠BCP, 且∠PBC = 40°, 则∠PDC = __________度.
4. 一次函数y = kx＋b, 当－3≤x≤1时, 对应的y的值为1≤y≤9, 则kb的值为________.
5. 设f (x) = ax＋
(1－x) (a＞0), 则当0≤x≤1时, f (x)的最小值g (a)为______.
6. 已知三条直线: y =3x
, y =
x＋1, y = －x＋4, 那么这三条直线所围成的封闭图形的面积等于__________.
7. 如果函数y = x＋2＋1－x＋x的值随x的值的增大而增大, 那么x取值的范围是____________.
8. 某环形跑道上顺时针排列有4所中学: A1、A2、A3、A4, 它们顺次有彩电15台, 8台, 5台, 12台, 为使各校的彩电数相同, 允许一些中学向相邻中学调出彩电, 则满足要求的调配方案中调出彩电台数最少时的台数为___________台.
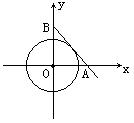9. 设动直线通过第一象限与x轴的交点为 (x, 0),
与y轴的交点为 (0, y), 如果x＋y = m (m为大于零的
常数), 以坐标原点为圆心的圆O外切于直线AB,
则⊙O半径R的最大值为__________.
10. 已知一次函数f (x) = ax＋b经过点(10, 13), 它在x轴上的截距是一个质数, 在y轴上的截距是一个正整数, 则函数的个数有_________个.
第二试
一、某家电生产企业根据市场调查报告, 决定调整产品生产方案, 准备每周 (按120个工时计算) 生产空调器、彩电、冰箱共360台, 且冰箱至少生产60台, 已知生产这些家电产品每台所需工时和每台产值如下表:
| 家电名称 | 空调器 | 彩电 | 冰箱 |
| 工时 |
|
|
|
| 产值 (千元) | 4 | 3 | 2 |
问每周应生产空调器、彩电、冰箱各多少台, 才能使产值最高? 最高产值是多少(以千克为单位)?
二、已知△ABC中, BC = a, AB = c, ∠B = 30°, P是△ABC内一点, 求PA＋PB＋PC的最小值.
三、已知直线L1: y = 4x和点P(6, 4), 在直线L1上求一点Q, 使过P, Q的直线与直线L1以及x轴在第一象限内所围成的三角形面积最小.