初中数学夏令营赛前模拟试题（五）
第一试
1. 已知 AB为半圆的直径, 其弦AF, BE 相交于Q, 过E、F分别作半圆的切线得交点P, 求证: PQ⊥AB.
2. 某地为促进淡水鱼养殖业的发展, 将价格控制在适当范围内, 决定对淡水鱼养殖提供政府补贴, 设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克, 根据市场调查, 当8≤x≤14时, 淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系:
P = 1000(x + t－8) (x≥8, t≥0)
Q = 500
(8≤x≤14)
(1)将市场平衡价格表示为政府补贴的函数, 并求出函数的定义域;
(2)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
3. 证明任意11个无穷小数中,一定可以找到两个小数,它们的差或者含有无穷多个数字0, 或者含有无穷多个数字9.
第二试
1. 若对任何实数a, 关于x的方程x2－2ax－a＋2b=0都有实数根, 求实数b的取值范围.
2. 已知在梯形ABCD中, AD∥BC, 点E、F分别在AB、DC边上, 且EF∥BC, 如果
, AD=m, BC=n, 求EF的长.
3. 已知a为整数, 4a2－12a－27是质数, 求a的值.
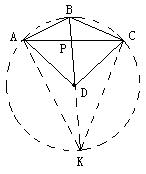4. 如图所示, 在凸四边形ABCD中, 已知
∠BAC = 25°, ∠BCA = 20°, ∠BDC = 50°,
∠BDA = 40°, 若四边形对角线AC, BD相交于
点P, 求∠CPD的度数.
5. 若某整数x的平方等于四个连续奇数的积, 求这种整数x的所有可能值之积.
6. 设M是边长为2的正三角形ABC的边AB上的中点, P是边长BC上的任意一点, 求PA＋PM的最小值.
7. 已知: a、b、c、d、e是实数, 满足a＋b＋c＋d＋e = 8, a2＋b2＋c2＋d2＋e2 = 16. 试确定e的最大值.
8. 有一化肥厂生产甲、乙两种混合肥料, 生产1车皮甲种肥料或1车皮乙种肥料需要的主要原料和生产的利润分别为: 磷酸盐4吨, 硝酸盐18吨, 利润10000元或磷酸盐1吨, 硝酸盐15吨, 利润5000元, 工厂现有库存磷酸盐10吨, 硝酸盐66吨, 应生产甲、乙种肥料各多少车皮可获最大利润?
9. 因为n, k均为正整数, 且
; 若对某一给定的正整数n, 只有唯一的一个正整数k使不等式成立, 求所有符合要求的正整数n中的最大数和最小数.
10. 当任意k个连续的正整数中都必有一个正整数, 它的数字之和是11的倍数时, 我们把其中每个连续k个正整数的片断都叫做一条长度为k的“龙”, 求最短的“龙”的长度.