2002年全国初中数学竞赛----辽宁省预赛试卷
一、选择题
1、已知点P的坐标为(x, y)且
，则点P关于原点的对称点P的坐标是( )
A、(-1，
) B、(-1，
) C、(1，) D、(1，)
2、已知α是锐角，且tgα=
，那么下列各式中正确的是( )
A、60°＜α＜90° B、45°＜α＜60°
C、30°＜α＜45° D、0°＜α＜30°
3、内接于半径为1的圆的正方形的面积是( )
A、
B、 C、2
D、4
4、设a、b为两圆半径，c为圆心距，且方程x2-2ax+b2=c(b-a)有两个相等的实数根，则这两个圆( )
A、相交 B、内切 C、相等 D、相等或外切
5、设
，
，
，则a，b，c之间的大小关系是( )
A、c＞b＞a B、a＞c＞b C、b＞a＞c D、a＞b＞c
6、制作一个圆锥模型，其侧面是用一个半径为9cm，圆心角为240°的扇形铁皮围成的，则圆锥底面半径为( )
A、4cm B、3cm C、6cm D、12cm
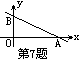7、右图是一次函数
的图象，那么△AOB的面积等于( )
A、
B、
C、
D、
8、平面上有O和I两点，以O为外心，I为内心的三角形( )
A、只能画出一个 B、只能画出2个
C、最多画出3个 D、能画出无数个
9、二次函数y=x2+mx+n中，如果m-n=0，那么它的图象一定经过点( )
A、(-1，-1) B、(1，-1) C、(-1，1) D、(1，1)
10、已知a为非负整数，若关于x的方程
至少有一个整数根，则a可以取值的个数为( )
A、1 B、2 C、3 D、4
二、填空题
11、解方程
时，若设
，则原方程可化为关于y的一元二次方程是______。
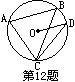12、如图⊙O为正△ABC的外接圆，OD∥AB(其中D为外接圆上的点)，则∠BCD=______度。
13、如果方程x2+(k2-4)x+k+1=0的两实根互为相反数，那么k=______。
14、已知半径为1cm和2cm的两个圆外切于点P，则点P到外公切线的距离为______。
15、若一次函数y=3x+b和反比例函数y=
的图像有两个交点，当b=______时，有一个交点的纵坐标为6。
16、在△ABC中，O是外心，I是内心，若∠BOC=100°，则∠BIC的度数是______。
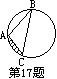17、如图⊙O的半径为1，圆周角∠ABC=30°，则图中阴影部分的面积为______。
18、已知定圆⊙O1半径为7cm，动圆⊙O2半径为4cm，若⊙O1与⊙O2内切，那么⊙O2的圆心轨迹是______。
19、已知
，
，
，……
(a，b为正整数)，请推测a=______，b=______。
20、已知方程m2x2-(4m+3)x+4=0有两个不相等的实数根x1、x2，设S=
，则S的取值范围是______。
三、21、阅读下面一题及解答过程，请判断是否正确？若不正确，请指出错在哪一步？并写出正确的解答过程。
化简：
解：=
==
=
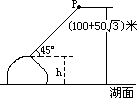
22、如图，在山顶A处望见一艘飞艇停留在湖面上空(100+50
)米处，观察到飞艇底部标志P处的仰角为45°，又观其湖中之像的俯角为60°，试求山高h(观察时湖面处于平静状态)。
四、23、某汽气装配厂计划在规定的时限内组装汽车21辆，组装了6辆汽车后，又追加了组装5辆汽车的订单，要求交贷时间不超过原来规定的期限，通过挖潜改革，提高工效，平均每天比原计划多组装2辆汽车，结果提前1天交货。问追加订单后，平均每天组装多少辆汽车？请用两种方法列出相应未知数的方程，并解答其中的一个。
五、24、某果品公司欲请汽车运输公司或火车货运站将60吨水果从A地运到B地，已知汽车和火车从A地到B地的运输路程均为S千米，这两家运输单位在运输过程中，除都要收取运输途中每吨每小时5元的冷藏费外，要收取的其它费用及有关运输资料由下表给出：
| 运输工具 | 行驶速度(千米/时) | 运费单价(元/吨千米) | 装卸总费用(元) |
| 汽车 | 50 | 2 | 2500 |
| 火车 | 80 | 1.7 | 2310 |
(1)请分别写出这两家运输单位运送这批水果所要收取的总费用y1元和y2元(用含S的式子表示)；
(2)若S=50，为减少费用，你认为果品公司应选择哪家运输单位运送这批水果更合算？(说明：“1元/吨千米”表示“每吨每千米1元”)