2002年湖北省数学竞赛试
（2002年1月3日上午9：00----11：00）
一、选择题：（本题共6小题，每小题5分，共30分）
1、已知是正数，且
=1，则
等于（
）
（A）5 （B）3 （C）1 （D）－3
2、如果某商品进价降低5%而售价不变，利润可由目前的a%增加到（a+15%），则a的值为（ ）
（A）185 （B）175 （C）155 （D）145
3、在直角坐标系中，已知A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P共有（ ）个
（A）1个 （B）2个 （C）3个 （D）4个
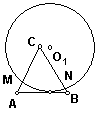4、为了调查学生的身体状况，对某校毕业生进行了体检，在前50名学生中有49名是合格的，以后每8名中有7名是合格的，且该校毕业生体检合格率在90%以上，则该校毕业生的人数最多有（
）
（A）180 （B）200 （C）210 （D）225
5、如图，圆的半径等于正三角形ABC的高，此圆在沿底边AB滚动，
切点为T，圆交AC、BC于M、N，则对于所有可能的圆的位置而言，
MTN弧的度数（ ）
（A）从30°到60°变动 （B）从60°到90°变动
（C）保持30°不变 （D）保持60°不变
6、用四条线段a=14，b=13，c=9，d=7作为四条边构成一个梯形，则在所构成的梯形中，中位线的长的最好大值是（ ）
（A）13．5 （B）11.5 （C）11 （D）10.5
二、填空题：（本题共6小题，每小题5分，共30分）
7、 已知
,则
8、 如图，在△ABC中AB=5，AC=13，边BC上的中线AD=6，则BC的长是
9、 与铁路平行的一条公路上有一行人与骑车人同时向南行进，行人的速度是每小时3。6km
骑车人的速度是每小时10。8km，如果一列火车从他们背后开来，它通过行人的时间是22秒，通过骑自行车的人的时间是26秒，则这列火车的身长是 m
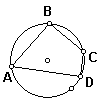10、如图，在圆内接四边形ABCD中，∠A=60°，
∠B=90°，AB=2，CD=1，则BC=
11、如图，在平行四边形ABCD中，M、N为AB
的三等分点，DM、DN分别交AC于P、Q两点，
则AP：PQ：QC=
三、解答题：（本题共3小题，每小题20分，共60分）
13、已知关于x的方程
（1） 求证：无论k取何实数值，方程总的实数根；
（2） 若等腰三角形ABC的一边长a=6，另两边长b、c恰好是这个方程的两个根，求此三角形的周长。
14、如图，△ABC的三边满足关系BC=
（AB+AC），O、I分别为△ABC的外心、内心，
∠BAC的外角平分线交⊙O于E，AI的
延长线交⊙O于D，DE交BC于H，
求证：（1）AI=BD
（2）OI=AE
15、观察按下列规则排成的一列数：
，，
，
，
，
，
，
，
，
，
，
，
，
，
，
，…
（1） 在（*）中，从左起第个数记为F（m），当F（m）=
时,求m的值和这m个数的积
（2） 在（*）中，未经约分且分母为2 的数记为c，它后面的一个数记为d，是否存在这样的两个数c和d，使cd=，如果存在，求出c和d；如果不存在，说明理由。
答案：
一、B、A、D、C、D、D；二12， 2
， 286 ，2
-2， 5：3：12， 179，
三、13、16或22
14、作IG⊥AB，连结BI，则AG=（AB+AC－BC），再证△AGI≌△BHD
15、（1）、分组：（），（，），（，，），（，，，），（，，，，），（，…），…（
，，
，…，
）。当F（m）=时，m=
积为：
，（2）、c为某组倒数第二个数，d为每组最后一个数，设它们在第n组c= 
, d=
= c=
, d=