北师大八年级下学期数学期末测试试题
时间120分钟 满分120分
班级 学生 成绩
一、选择题(3分×10=30分)
1、 解不等式
≥2 ，它的解在数轴上表示为
( )
 | |||
 | |||
0 1 2
0 1 2
A B
|  |
0 1 2
0 1 2
C D
2、 下列多项式中，能用提公因式的是 （ ）
A 
B 
C
D 
3、
的最小整数解为
（
）
A -1 B 0 C 2 D 3
4.分式
的值为0，则x的取值为
A 
B 
C 或
D 或
5、现用甲、乙两种运输车将46吨抗旱物资运往灾区，甲种运输车载重5吨，乙种运输车载重4吨，安排车辆不超过10辆，则甲种运输车至少应安排 （ ）
A 4辆 B 5辆 C 6辆 D 7辆
6、下列命题中错误的是 （ ）
A 有一个角为
的两个等腰三角形是相似形
Ｂ 底角为
的两个等腰三角形是相似形。
Ｃ 两个等腰直角三角形是相似三角形。
Ｄ 两个等边三角形是相似三角形。
7、如图，D是AB边上一点，E是AC上一点，AB=9，AC=6，AD=3，若要使△ADE与△ABC相似，则AE的长为
（ ）
A
A
2
B 
D· E
C 
D 2或
B
C
8、若
是完全平方式，那么
（ ）
A 7 B 5 C -1 D 7 或 -1
9、已知a、b、c为△ABC的三边，且满足
，则△ABC的形状是（ ）
Ａ 等腰三角形 B 直角三角形
C 等腰直角三角形 D 等腰或直角三角形
10、解方程
会产生增根,则
等于
(
)
A -10 B -10或-3 C -3 D -10或-4
二、填空题。（3分×8分=24分）
11、命题“若
”的条件是（
），该
命题为（ ）命题。（填“真”或“假”） A
12、如图，在△ABC中，点D是射线BC上的任意一点，
F
DF交AB与F，交AC于E，则 E
∠FEC与∠AFE的大小关系是（
）
D
C
B
13、计算：
（
），
（ ）
14、在△ABC中，点D、E分别在边AB、AC上，DE∥BC，AD=1，BD=2，则
：
（ ）
15、为了解我市八年级学生的视力状况，较合理的调查方式是（ ）。
16一组数据0，-1，2，-2，1的极差是（ ），方差是（ ）。
17、已知
（ ），B=（
）
18、已知
…，
（ ），由此可得
（
）。
三、解答题（满分66分）
19、（6分） 分解因式：
、① 
② 
20 （ 8分）解不等式（组）
① 
② 
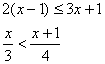
21、（5分）解方程
22、先化简，再求值。
23、（8分）如图，在△ABC中，AD、CE是两条高，连结DE，如果BE=2，AE=3，CE=4在不添加任何辅助线和字母的条件下，写出三个正确的结论（要求：分别为边
的关系、角的关系、三角形相似等），并对其中一个结论给予证明。
C
D
A
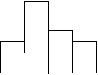
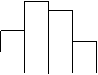
E B
24、（10分）在一次环保知识测试中，二年级一班的两名学生根据班级成绩（分数为整数）分别绘制了组距不同的频率分布直方图，如图1、图2。已知图1从左到右每个小组的频率分别为：0.04、0.08、0.24、0.32、0.20、0.12，其中68.5～76.5小组的频数为12
图2从左到右每个小组的频数之比为1：2：4：7：6：3：2，请结合条件和频率分布直方图回答下列问题。
（1） 二年级一班参加测试的人数为多少？
（2） 若这次测试成绩80分以上（含80分）为优秀，则优秀率是多少？
（3） 若这次测试成绩60分以上（含60分）为及格，则及格率是多少？
 |  |
52..5 60.5 68.5 76.5 84.5 92.5 100.5
51 .5 58.5 65.5 72.5 79.5 86.5 93.5 100.5
25、某一工程，在工程招标时，接到甲、乙两个工程队的投标书，施工一天，需付甲工程队工程款1.5万元，乙工程队工程款1.1万元，工程领导小组根据甲乙两队的投标书测算，可有三种施工方案：
（1）甲队单独完成这项工程刚好如期完成；
（2）乙队单独完成这项工程要比规定日期多5天；
（3） 若甲、乙两队合作4天，余下的工程由乙队单独做也正好如期完成，在不耽误工期的前提下，你觉得哪一种施工方案最节省工程款？
26、（12分）某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房的成本和售价如下表
| A | B | |
| 成本（万元/套） | 25 | 28 |
| 售价（万元/套） | 30 | 34 |
（1`）该公司对这两种户型住房有哪几种建房方案？
（2） 该公司如何建房获得利润最大？
（3） 根据市场调查，每套B型住房售价不会改变，每套A型住房的售价将
会提高a万元（a﹥0），且所建的两种住房可全部售出，该公司又将如何建房
获得利润最大？