5.1~5.4 每周干家务活的时间、数据的收集、频数与频率、数据的波动(B卷)
班级:_______姓名:_______得分:_______发展性评语:___________
一、请准确填空(每小题3分,共24分)
1.“在一次考试中,考生有2万多名,如果为了得到这些考生的数学平均成绩,而将他们的成绩全部相加再除以考生总数,那将是十分麻烦的,那么怎样才能了解这些考生的数学平均成绩呢?”
“通常,在考生很多的情况下,我们是从中抽取部分考生(比如说500名)的成绩,用他们的平均成绩去估计所有考生的平均成绩.”
上述文字表达了统计中用样本平均数估计总体平均数的统计思想.其中,总体指的是________,个体指的是________.
请你用简洁的语言,举一个在实际生活中,运用同样思想解决问题的例子,写在下面:________.
答案:2万多名考生的数学成绩 每位考生的数学成绩(符合实际的例子)
2.已知样本x1,x2,x3,…,xn的方差为2,则样本2x1+1,2x2+1,…,2xn+1的方差为________.
答案:4S2=8
3.把容量是50的样本分成6组,其中有1组的频数是14,有2组的频数均为10,有2组的频率均是0.14,则另一组的频数是________,频率是________.
答案:2 0.04
4.图1是某班50名学生身高频率分布直方图(精确到1厘米),从左边起第一、二、三、四个小长方形的高的比是1∶3∶5∶1,那么身高150厘米以下(不含150厘米)的学生有______人;身高160厘米及160厘米以上的学生占全班学生人数的______%.
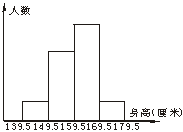
图1
答案:5 60
5.为了考察一个养兔场兔的生长情况,从中抽取5只,称得它们的重量如下(单位:千克):3.0,3.2,3.4,3.3,3.1.在这个问题中,样本的方差是________.
答案:0.02
6.某班通过一次射击测试,在甲、乙两名同学中选出一名代表班级参加校射击比赛,这两名同学在相同情况下射靶5次,所测得的成绩分别如下(单位:环):
甲:7,8,9,8,8;乙:5,10,6,9,10.
根据测试成绩,认为应该由________代表班级参加比赛.
答案:甲
7.从总体中取m个a,n个b,p个c组成一样本,那么这个样本的容量为________,n个b的频率是________.
答案:m+n+p ![]()
8.2004年某市某居民楼住宅小区物业管理部门就该部门负责的居民对物业管理满意程度问题进行了抽样调查,结果如图2所示.据此,可估计2004年该住宅小区居民中对物业管理水平表示认可的约占______%.
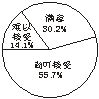
图2
答案:85.9
二、相信你的选择(每小题3分,共24分)
9.频数分布直方图中小长方形的高等于
A.频数与组距的比值 B.相应各组的频数
C.相应各组的频率 D.频数与数据总数的比值
答案:A
10.某气象站为了解某一天12小时的温度变化情况,每两小时测量记录一次,这个问题中,样本容量是
A.12 B.6 C.2 D.1
答案:B
11.下列说法错误的是
A.一组数据的方差必须是非负数
B.将一组数据中的每一个数据都加上(或都减去)同一个常数后,方差恒不变
C.在频率分布直方图中,每个小长方形的面积等于相应小组的频率
D.一个容量为80的样本最大值是140,最小值是50,取组距为10,则可以分成9组
答案:D
12.某学校参加数学竞赛的有400人,其中成绩在78~80之间的有80人,则这个分数段的频率是
A.0.2 B.0.25 C.0.5 D.80
答案:A
13.下列说法错误的个数有
①一组数据的标准差是它的方差的平方根
②数据x1,x2,…,xn的平均数是![]() ,那么(x1-
,那么(x1-![]() )+(x2-
)+(x2-![]() )+…+(xn-
)+…+(xn-![]() )=0
)=0
③数据-1,0,2,1,2,0的众数是2
④数据0,-1,1,-2,1的中位数是1
A.4个 B.3个 C.2个 D.1个
答案:B
14.在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示,请根据此表回答下列问题.
| 年龄段 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
| 人 数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
样本年龄在60岁以上(含60岁)的频率是
A.0.16 B.0.08 C.0.14 D.16
答案:A
15.要了解全市八年级学生身高在某一范围内所占比例的大小,需知道相应样本的
A.平均数 B.方差 C.众数 D.频率分布
答案:D
16.在全校八年级数学竞赛中,有15人参加,成绩排在前8名的有奖,小明参加这次竞赛考试,要想知道自己是否获奖,他应注意下列数据中的
A.平均数 B.中位数 C.众数 D.方差
答案:B
三、考查你的基本功(共19分)
17.(8分)某居民小区开展节约用水活动,成效显著,据对该小区200户家庭用水情况统计分析,3月份比2月份节约用水情况如下表所示:
| 节水量(立方米) | 1 | 1.5 | 2 |
| 户 数 | 20 | 120 | 60 |
(1)填空:节水量的众数是________.
(2)求3月份平均每户节约用水多少立方米?
答案:(1)1.5 (2)1.6
18.(11分)某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下.
| 每人销售的件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人 数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位销售人员该月销售量的平均数、中位数和众数;
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
答案:(1)![]() =
=![]() (1800+510+3×250+5×210+3×150+2×120),
(1800+510+3×250+5×210+3×150+2×120),![]() =320.
=320.
中位数:210,众数:210.
(2)不合理.月销售额定为210件合适,这是大部分能完成的月销售量.
如定在320件,15人中只有两人能完成任务.
四、生活中的数学(共22分)
19.(11分)图3是我国运动员从1992~2004年在奥运会上获得奖牌数的统计图,请你根据统计图提供的信息,回答下列问题.
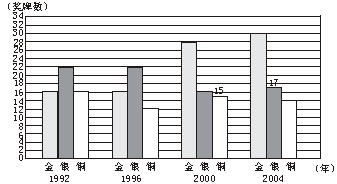
图3
(1)从1992~2004年四届奥运会我国运动员共获奖牌多少枚?
(2)哪届奥运会我国运动员获得的奖牌总数最多?
(3)根据以上统计,预测我国运动员在2008年北京奥运会上大约能获得多少枚奖牌?
答案:(1)226.
(2)2004年获奖牌63枚,在这四届中最多.
(3)七十余枚.
20.(11分)甲、乙两人在相同条件下各自的射靶成绩情况如图4所示.
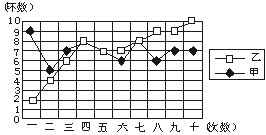
图4
(1)请填写下表:
| 平均数 | 方差 | 中位数 | 命中9环以上次数 | |
| 甲 | 7 | 7 | ||
| 乙 | 7 | 7.5 |
(2)请从平均数和方差相结合的角度,对这次测试结果进行分析.
答案:(1)甲 1.2 1
乙 5.4 3
(2)甲、乙二人平均数相同,但S甲2<S乙2.
∴甲的成绩比较稳定;乙的成绩波动较大.
五、探究拓展与应用(11分)
21.观察下列三组数据(三组数据个数一样),解答下列问题:
①1,2,3,4,5,6,…,xn;
②3,4,5,6,7,8,…,yn;
③4,6,8,10,12,14,…,zn.
(1)根据你观察的结果,用含xn的代数式分别表示yn和zn;
(2)若设①组数据的平均数和方差分别为![]() 1,S12,则②③组数据的平均数和方差各为多少?由此,你能得出什么规律?与同伴交流.
1,S12,则②③组数据的平均数和方差各为多少?由此,你能得出什么规律?与同伴交流.
解:(1)yn=xn+2,zn=2xn+2.
(2)![]() S22=S12,
S22=S12,![]() , S32=4S12.
, S32=4S12.
规律:①当一组数中每一个数都加上同一个常数,构成新的一组数据的平均数也等于原数据平均数与这个常数的和,而方差不变 ②当一组数据中每一个数变为原来的n倍,新数据的平均数也是原数据平均数的n倍,方差变为原方差的n2倍.