【巩固练习】
§4.3 菱形
1. 菱形中较大角是较小角的3倍，高为5cm，则这个菱形的边长是___________。
2. 菱形周长为16cm，一对角线长4cm，则另一对角线长为___________。
3. 菱形的两条对角线长为6和8，则菱形的边长为___________，面积为___________。
4. 在边长为2的菱形ABCD中，∠B＝45°，AE为BC上的高，将△ABE沿AE所在的直线翻折后得△AB'E，那么△AB'E与四边形ABCD重叠部分的面积是___________。
5. 在菱形ABCD中，AB＝6cm，对角线BD＝6c m，则另一对角线AC＝___________cm。
6. 菱形ABCD中，∠DAB＝60°，AC＝
cm，则菱形ABCD的边长AB＝___________cm。
7. 菱形的周长为32cm，一个角的度数是60°，则两条对角线的长分别是（ ）
A. 8cm和
cm B.
4cm和
cm
C. 8cm和
D.
4cm和cm
8. 下列结论正确的是（ ）
A. 邻角相等的四边形是菱形
B. 有一组邻边相等的四边形是菱形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直平分的四边形是菱形
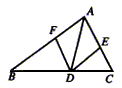
9. 如图所示，AD是△ABC的角平分线，DE∥AB，DF∥AC，四边形AEDF是菱形吗？说明理由。
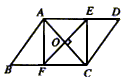
10. 如图所示，平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F，试说明AFCE是菱形。
§4.4 矩形、正方形
1. 正方形的边长为2，则它的对角线为____________。
2. 正方形的面积为9，则它的对角线为____________。
3. 正方形的对角线长为1，则它的面积为____________。
4. 矩形的面积为84，一边长为12，则它的对角线长为____________
5. 矩形的对角线长为8cm，对角线的夹角为60°，则这个矩形的边长分别为____________。
6. 矩形ABCD中，M是BC的中点，MA⊥MD，如果矩形ABCD的周长是48cm，则矩形的面积为____________。
7. E是正方形ABCD内一点且△EAB为等边三角形，则∠ADE＝____________。
8. 正方形具有而菱形不一定具有的性质是（ ）
A. 对角线互相平分
B. 对角线互相垂直
C. 对角线相等
D. 对角线平分一组对角
9. 矩形的边长为10cm和15cm，其中一个内角平分线分长边为两部分，这两部分为（ ）
A. 6cm和9cm B. 5cm和10cm
C. 4cm和11cm D. 7cm和8cm
10. 如图所示，矩形ABCD沿AE折叠，使点D落在BC边上的F点处，如果∠BAF＝60°，则∠DAE等于（ ）
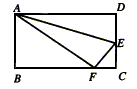
A. 15° B. 30° C. 45° D. 60°
§4.5 梯形
1. 梯形ABCD中，AD∥BC，AB＝DC＝8cm，BC＝15cm，∠B＝60°，则AD＝____________，梯形的面积为____________。
2. 在梯形ABCD中，AD∥BC，DE∥AB，△DEC的周长为10cm，BE＝5cm，则梯形的周长为____________cm。
3. 梯形ABCD中，AD∥BC，∠B＝72°，∠C＝48°，则∠A＝____________，∠D＝____________。
4. 等腰梯形上底6cm，下底8cm，高为3cm，则腰长为____________cm。
5. 在等腰梯形ABCD中，AC、BD相交于点O，则下图中有____________对全等三角形。
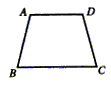
6. 如图所示，梯形ABCD中，AB＝CD，那么它的四个内角度数比可能为（ ）
A. 3：4：5：6
B. 4：5：4：5
C. 2：3：3：2
D. 2：4：3：3
7. 如图所示，在梯形ABCD中，AD∥BC，AB＝DC，∠D＝120°，对角线CA平分∠BCD，且梯形的周长为20，求AC的长以及梯形的面积S。
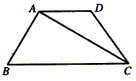
8. 如图所示，在等腰梯形ABCD中，AD∥BC，点E是BC延长线上的点，且CE＝AD，试判断△BDE的形状，并说明理由。
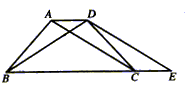
【练习答案】
§4.3 菱形
1. 
cm
2. cm
点拨：菱形对角线互相垂直平分。
3. 5，24
4. 
点拨：注意45°角的利用。
5. 
6. 3
7. C
点拨：以上各题均是利用等边三角形和菱形的性质。
8. D
9. 解：是菱形。理由如下：
∵DE∥AB、DF∥AC，∴四边形AFDE是平行四边形。
又∵∠FAD＝∠DAE，∴∠FDA＝∠EAD＝∠FAD，
∴AF＝FD，∴平行四边形AFDE是菱形。
10. 解：∵OA＝OC，∠AOE＝∠COF，∠EAO＝∠FCO，
∴△AOE≌△COF，∴AE＝CF。
又∵AE∥CF，∴四边形AFCE是平行四边形。
又∵EO是AC的垂直平分线，
∴EA＝EC，∴平行四边形AFCE是菱形。
§4.4 矩形、正方形
1. 
2.
3.
4. 
5.
6. 128（cm2） 7. 75°
8. C 9. B 10. A
§4.5 梯形
1. 7cm，
cm2
2. 20
点拨：DE∥AB，等于把梯形分成了一个平行四边形和一个三角形。
3. 108°，132°
4. 
5. 3
6. C
点拨：等腰梯形同一底上的两个底角相等。
7. 解：
，∵∠D＝120°，且CA平分∠BCD，AD∥BC，
∴∠BCA＝∠DAC＝∠DCA，∴DA＝DC，∵∠BCA＝30°，∠B＝60°
∴∠BAC=90°，∴BC=2AB，设AB＝x，则3x＋2x＝20，x＝4，
∴2AB=BC=8 
，梯形的高为△ABC中BC边上的高为
，
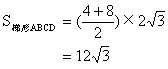
8. 解：△BDE是等腰三角形。理由如下：∵AD∥CE且AD＝CE，
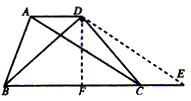
∴四边形ACED是平行四边形，∴AC＝DE
又∵ABCD是等腰梯形，∴BD＝AC，∴BD＝DE，
∴△BDE是等腰三角形。
点拨：平移对角线也是梯形中重要的作辅助线的方法之一。