图形的平移和旋转(无答案)[上学期]

 

 八年级(上)数学单元目标检测题(A)

　　　　　　　　　　　　　　   (图形的平移与旋转)

姓名:　　　　　   班别:　　　　  : 座号:　　　　  评分:　　　　　

一.　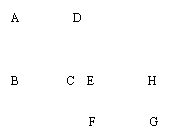选择题( 本大题共6小题, 每小题4分,共24分)

1.如图,正方形EFGH是由正方形ABCD平移

　得到的, 则有(　)

A. 点E和B对应　　　B. 线段AD和EH对应

C. 线段AC和FH对应  D. ∠B和∠D对应

2.如图,共有5个正三角形,从位置来看,(　)是由

　左边第一个图平移得到的.

　　　　　　　  A　　　　　  B　　　　　  C　　　　　　  D

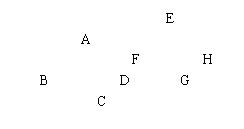
3.如图,四边形EFGH是由四边形ABCD平移

得到的,已知AD=5,∠B=70⁰,则(　)　　　　　　　　　　　　　　 

A. FG=5, ∠G=70⁰　　 B. EH=5, ∠F=70⁰

C. EF=5, ∠F=70⁰　　 D. EF=5. ∠E=70⁰

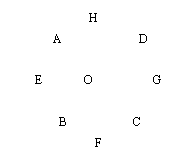　 4. 如图,所给的图案由ΔABC绕点O顺时针

旋转(　)前后的图形组成的.

　　A. 45⁰、90⁰、135⁰　　　　B. 90⁰、135⁰、180⁰　　

　　C.45⁰、90⁰、135⁰、180⁰、225⁰

　　D.45⁰、135⁰、225⁰、270⁰.

　 5. 下列说法正确的是(　)

　　A.平移不改变图形的形状和大小,而旋转则改　　

　 变图形的形状和大小

B.平移和旋转的共同点是改变图形的位置

C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离

D.由平移得到的图形也一定可由旋转得到

　 6.将图形按顺时针方向旋转90⁰后的图形是(　)　　　　　 

 

　　　　A　　　　　　　　 B　　　　　　　  C　　　　　　　　　  D

 二. 填空题(本大题共6小题,每小题4分,共24分)

　 7.ΔABC经过平移得到ΔDEF,并且A与D,B与E,C与F是对应点, AD=3,

　则BE=　　,AD与BE的位置关系是　　, AB与DE的位置关系是　　.

　 8.如图,左图是一个五边形,先把左图

沿　　 方向平移,再沿　　 方向平移

便可得到右图.

　 9.钟表上的分针绕其轴心旋转,分针经过15

　分后,分针转过的角度是　　;分针从12出发,转过150⁰,则它指的数字是　 .

　 10.如所给的图案,可看作由“基本图案”：　　 

旋转　  度得到的，旋转的两个图形必　　　 。

　 11.如图,绕点O旋转的两个图形的对应点

　M与N到旋转中心O的距离　　(相等或不相等).

　 12.如所给图案,可看作是

　图形“　　 ”经　　次平

　移得到的，也可看作是图形

　“　　　”绕中心旋转　　　　　　　　

　得到，还可看作是图形“　　　　　 ”经轴对称得到整个图案的。

三. 解答题（本大题共5小题，共52分）

　13．怎样将右图中的甲图案变成乙图案?

（10^/）

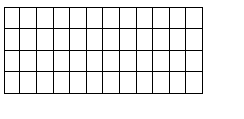
　14.作出图中三角形先向右

向右平移5格,再顺时针旋转

60⁰的图案.（10^/）

15.观察右图中的图案,它是

否可看作是某个“基本图形”

经过平移、旋转或轴对称而形

成的？（10^/）

　16.右图中的图案绕中心旋转多少度后

能和原来的图案相互重合?（10^/）

　17.分析右面图案形成过程,并利用一个圆,

通过平移、旋转和轴对称设计一个图案，说

明你的设计意图。（12^/）

　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　

　　　　　　　　　　　　　　　　　　　　　　　

八年级(上)数学单元目标检测题(B)

　　　　　　　　　　　　　　   (图形的平移与旋转)

姓名:　　　　　   班别:　　　　  : 座号:　　　　  评分:　　　　　

一. 选择题( 本大题共3小题, 每小题4分,共12分)

1.　　下列运动是属于旋转的是(　)

A.滾动过程中的篮球的滚动　　　B.钟表的钟摆的摆动

C.气球升空的运动　　　　　　  D.一个图形沿某直线对折过程

2.　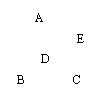　如图,ΔABC和ΔADE均为正三角形,则图中

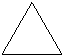
 可看作是旋转关系的三角形是(　)

　 A. ΔABC和ΔADE　　　 B. ΔABC和ΔABD

　 C. ΔABD和ΔACE　　　 D. ΔACE和ΔADE

3.　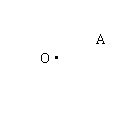　如图,过圆心O和圆上一点A连一条曲线,

　将曲线OA绕O点按同一方向连续旋转三次,每

　次旋转90⁰,把圆分成四部分,则(  )

　 A. 这四部分不一定相等　　B. 这四部分相等

　 C. 前一部分小于后一部分　D. 不能确定

二. 填空题(本大题共3小题,每小题4分,共12分)

　7.矩形ABCD绕点　　　旋转后能与矩形CDEF重合.

　8.如图,图中的图案可看作是　 个小正方形连续平移

 　　 次,平移前后所有的图形共同组成的图案.

　9.一个正三角形绕其一个顶点按同一方向连续旋转五

 次,每次转过的角度为60⁰, 旋转前后所有的图形共同组成的图案是　　　 .

三. 解答题（本大题共6小题，第10题16分,其余每题12分共76分）

　10.①如图,将一个矩形ABCD绕BC边的中点O旋转90⁰后得到矩形EFGH.已

知AB=5cm,BC=10cm,求图中阴影部分面积.

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

 

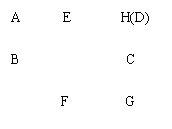
②将RtΔABC沿斜边AB向右平移5cm,得到

RtΔDEF.已知AB=10cm,BC=8cm,求图中阴影部分

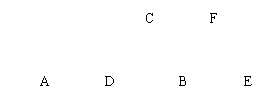三角形的周长.　　　　　　　　 　　　　　　

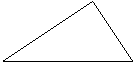
　 11.如图,作出ΔABC绕点O旋转120⁰的图形.

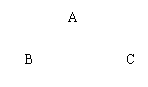
　　12.利用两个圆、两个正三角形通过2次平移或旋转或轴对称设计一个图案，

 并说明你的设计意图。

13.分析下图的旋转现象(写出所有组合的旋转现象).

14.在四边形ABCD中,∠ADE=∠B=90⁰,DE⊥AB,垂足为E,且DE=EB=5,请用

 旋转图形的方法求四边形ABCD的面积.

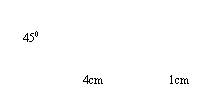
15.如图,河两边有甲、乙两条村庄,现准备建一座桥,桥必须与河岸垂直,

 问桥应建在何处才能使由甲到乙的路程最短?请作出图形,并说说理由.